国家公務員総合職（化学・生物・薬学）H27年 問16解説

　問 題　　　　　

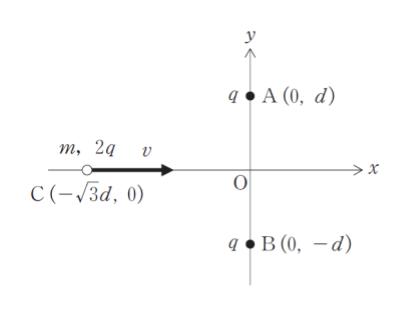
図のように、真空中の xy 平面上の点 A (0,d) 及び点 B (0, －d) に電荷 q の点電荷が固定されている。点C (－√ 3d , 0) から、質量 m、 電荷 2q の小球を x 軸の正の向きに速さ v で発射するとき、原点O (0, 0) に到達するために必要な v の最小値として最も妥当なのはどれか。ただし真空の誘電率を ε₀ とし小球に作用する重力は無視できるものとする。

なお、真空中において、電荷 Q_x の点電荷 X と電荷 Q_Y の点電荷 Y が距離 r 離れて置かれているとき、X、Y の間には F = Q_xQ_Y/4πε₀r² の静電気力が働き X Y の電気的な位置エネルギーをそれぞれ U_x,U_Y とすると、U_x、U_Y は無限遠を基準(r ＝∞ のとき U_x ＝ U_Y ＝ 0) として
U_x ＝ U_Y ＝ Q_xQ_Y/4πε₀r　で表される。

 

 

 

 

 

　解 説　　　　　

電気的な位置エネルギーとは、電位といえます。電位はスカラー量なので、点 A、点 B それぞれの点電荷が作る電位を単純に足し合わせたものが、点 C における電気的な位置エネルギーです。

各点電荷による電気的な位置エネルギーは、電荷 q,2q,距離が 2d なので

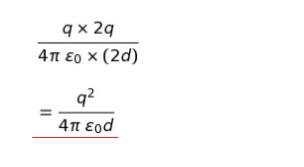
それぞれの点電荷による電気的な位置エネルギーを足し合わせると、２倍すればよいので

次に、到達したい原点 O の電気的な位置エネルギーを考えます。電荷 q,2q,距離が d で、それぞれの電荷による位置エネルギーを足し合わせると q²/πε₀d です。差を計算すると、以下のようになります。

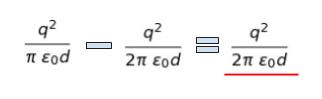
一方、質量 m、速さ v で発射された小球が持つ運動エネルギー K は、K = mv²/2 と表されます。位置エネルギーの差 ≦ 運動エネルギー　であれば、原点 O に到達すると考えられます。不等式を、v について解くと、以下のようになります。

以上より、正解は 4 です。