【クリアランス、全身クリアランス】
まず、クリアランスとは何か、クリアランスのイメージについて説明します。
クリアランス(CL と略します。)とは「薬物を取り除く能力を示す数値」 です。「薬物入りの血液を、一時間で何 L きれいにできるか示す数値」と考えると、イメージしやすいかもしれません。
他には、コンビニやスーパーで、カゴに品物を入れてレジに向かってくる人の流れ を考えてみてください。「カゴに入った品物」=「薬物」、「カゴを持っている人」=「血流」 のたとえです。クリアランスとは、「1時間で何人レジで捌けるか を示す数値」と考えてもよいと思います。
意味としては以上ですが、クリアランス という単語が出て来たら『薬物の消失速度=クリアランス×薬物濃度』・・・(1)という関係を、知識としてぜひ憶えておいてください。
レジの例えで言えば、クリアランス=人の数、薬物濃度=カゴの中の品物の個数 に対応します。式(1) の右辺は、例えでいうと、人の数 × カゴの中の品物の個数 だから「品物をレジで何個捌いたか」 という意味です。品物を捌いた個数は、薬物の消失速度 の例えになります。
次に、全身クリアランス(全身 CL) についてです。
人体において、薬物は様々な臓器で代謝を受けます。代謝において特に重要な臓器は、肝臓と腎臓です。そこで、全身のクリアランスは、肝臓のクリアランスと、腎臓のクリアランスの和だと考えます。式で表すと、以下になります。全身 CL = 肝臓 CL + 腎臓 CL。ここまでが、クリアランスの一般的な話です。
確認問題
1:クリアランスを一言で表すと?
2:全身CL=?+?
【肝クリアランス】
次に、肝クリアランスについて説明します。
肝クリアランスとは、肝臓において、薬物入りの血液を一時間で何 L きれいにできるか示す数値と考えればよいです。イメージは、下図になります。
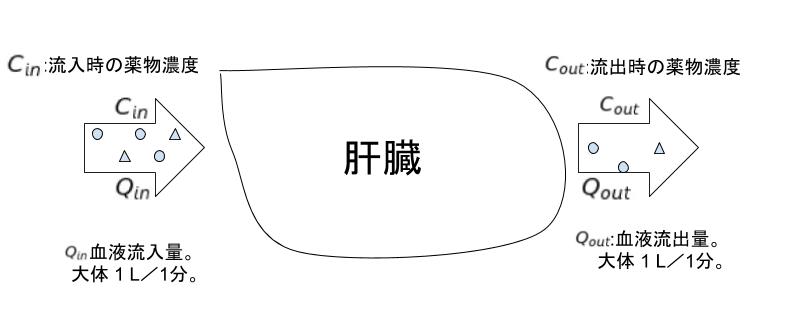
式で表すと、以下のようになります。

具体的な数で、2例考えてみましょう。
例1)肝臓に流入する血液量は大体 1 分間に 1 L なので1 時間で、 60 L です。Q = 60 (L/時) とします。薬物は一種類で、肝臓で完全に代謝されるとします。Cin として、適当に 10mg/L としましょう。完全に代謝されるから、Cout は、0 mg/L です。式(2)の右辺に代入してみると
肝CL = (60 × (10 – 0))/10 = 60 です。
例2)Qは、60(L/時)とます。薬物が完全に代謝されない場合を考えます。Cin = 10mg/L、Cout = 5mg/L とします。例1 と同様に考えれば、肝CL = (60 × (10 – 5))/10 = 30 です。
重要なポイントは、『肝クリアランスは、血流量を超えない』 という点です。(肝臓で薬物は代謝されるので、Cin よりも、Cout は小さくなります。すると、式中の『(Cin - Cout)/Cin』 は、0 ~ 1 の値をとります。よって、最大でも、Q × 1 にしかならない = 『肝クリアランスは、血流量を超えない』 という意味です。)
確認問題
1:肝クリアランスの式は?
2:肝クリアランスと血流量の大小関係は?
【肝固有クリアランス】
次に、肝固有クリアランス(肝固CL)について説明します。
これは、一言で表せば「血中タンパク質と薬物の結合を考慮した肝クリアランス」 です。肝臓において、実際に代謝を受けるのは、血中タンパク質であるアルブミンなどと結合していない、いわばフリー(free) の薬物です。
フリーの薬物は血流に乗って肝臓に到達し、肝組織の細胞膜を通過することで肝組織に分布し、そこで種々の酵素によって代謝を受けます。一方、フリーではなくタンパク質と結合している(binded)薬物は、肝組織へ移行することなくそのまます~っと流れていくだけです。
これは、初めのレジのたとえでいうならば、フリーの薬物 というのはカゴに入っている品物です。一方で、タンパク質付きの場合は、もう既に他で会計済みで袋に入っておりレジを通す必要がない品物です。にも関わらず、肝クリアランスは free と binded の区別をせずに薬物濃度として考えています。
具体的な数で考えるならば
薬物 A は 100 % フリー、薬物 B は 20 % フリー、80 % タンパク質と結合 とします。血液量 Q は、50 L/h とします。(60 L/h でないのは、計算の都合です。)これら2つの薬物の肝クリアランスが、ともに 10(L/h) と仮定します。つまり、薬物 A の肝クリアランスも、薬物 B の肝クリアランスも 10 L/h です。
さきほどのレジの例えで考えれば
薬物 A の肝クリアランスが示しているのは、『カゴに品物 A を入れてきた 50 人が流れてきた時、10 人を1時間で捌ける』 ということです。
一方、薬物 B のクリアランスが示しているのは
『品物 B をレジで通さなければならない客は 20 % の割合でしかないような、50 人がレジに流れてきた時に、10 人を1時間で捌ける』 ということです。
同じ 10 でも
意味が全く違うことがイメージできれば幸いです。
以上をふまえ
肝固有クリアランスがどのように表せるかについて、以下説明します。
クリアランスを考えるには薬物濃度が必要ですが、血中濃度ならまだしも肝組織における薬物濃度はよくわかりません。そこで、肝組織における薬物濃度を簡単なモデルで表すのが、well – stirred(ウェール スティアード) モデル です。(日本語にすれば よく混ざってるよモデル です。)このモデルのポイントは『肝組織の薬物濃度を(C out) × フリーな割合 (f) 』とした点です。
ここで式(1) を思い出してほしいのですが(『薬物の消失速度=クリアランス×薬物濃度』・・・(1))、(1)より、薬物濃度とクリアランスをかければ薬物の消失速度がわかるはずです。そして、モデルのおかげで、なぞのはずの肝組織における薬物濃度はわかります。(C out × フリーな割合 です。)。
ここで、肝固CL を仮定します。
すると、式(1)より、薬物の消失速度は
『肝固CL × フリーな薬物濃度(=f × C out)』と表すことができます。
まとめると
・肝固CL とは、タンパク結合を考慮したクリアランスです。
・well – stirred model を考えることで 『薬物の消失速度 = 肝固CL × f C out 』・・・(3)という関係がなりたつ ということになります。ここまではよろしいでしょうか。
【肝CL と 肝固CL の関係】
最後に、肝クリアランスと肝固有クリアランスの関係についてまとめます。
肝クリアランスに関する式を再度以下に示します。
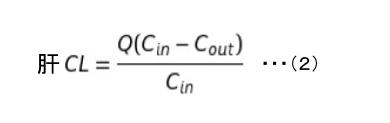
これを、式(3) 『薬物の消失速度 = 肝固CL × f C out 』 と連立して、1つの式にします。
まず、(3)は、Qin(Cin-Cout) = 肝固CL × f Cout です。
この式を Cin について解きます。
QinCin = 肝固CL × f Cout + QinCout
の両辺を Qin で割ることで
Cin = (肝固CL × f +Qin)Cout / Qin ・・・(3)’
と解けます。
(3)’ を(2)に代入して整理します。
先に「(2)式の右辺と左辺を入れ替えた上で両辺を Cin で割っておく」と、代入して整理した時の見通しが立ちやすいと思います。すなわち、「肝CL = Qin – QinCout/Cin」・・・(2)’ としておきます。
(2)’の Cin に(3)’を代入し、整理することで
『肝CL=(Qin・f・肝固CL)/Qin + f・肝固CL』・・・(4)
という関係が導かれます。
(4)の右辺は
大雑把に見れば「ab/a+b」という式になっており、基本的な 2 変数関数と見て性質を数学的に解析することが容易な形であるという特徴があります。
重要なポイントが、(4)の式の近似です。
すなわち、Q << f・肝固CL の時
(4)右辺の分母は、ほぼ f・肝固CL と見なせるため、『肝 CL ≒ Qin』と近似できます。このような薬物は、血流量依存性の薬物と分類されます。代表例は、ニトログリセリン、リドカイン、プロプラノロール などです。
これらの薬物は、肝機能の変化であまり肝 CL は変化しません。一方で、血流量、つまり心機能の低下に伴い肝 CL が低下して血中濃度が高くなる薬物といえます。
また、Q>>f ・肝固CL の時
(4)右辺の分母は、ほぼ Q と見なせるため、結局(4)式は、『肝CL ≒ f・肝固CL』 と近似できます。このような薬物は、代謝能依存性の薬物と分類されます。代表例は、ワーファリン、フェニトインなどです。
特に well – stirrede model について
理解が深まる練習問題
97-173,103-172,106-175,107-176

コメント