国家公務員総合職（化学・生物・薬学）R1年 問39解説

　問 題　　　　　

半径 r、温度 T の等温球面と半径 r +dr、温度 T+dT の等温球面で囲まれた厚さ dr の球殻を考える。球面を半径方向に流れる単位時間当たりの熱量 Q は，熱伝導率を k、球面の面積を A とするとフーリエの法則より

で与えられる。半径 r と温度 T に関する境界条件で積分すると、球殻を半径方向に流れる単位時間当たりの熱量を求めることができる。

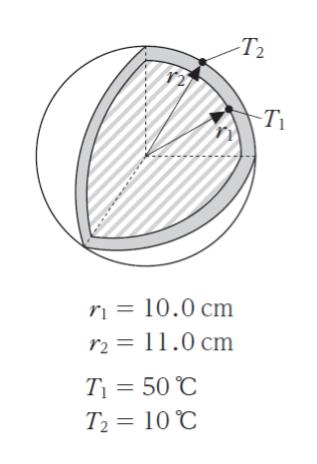
いま、図のように半径 10.0 cm のゲル状蓄熱剤を内包した球状カプセルにおいて、カプセル内温度及び外壁温度はそれぞれ 50 ℃ 及び 10 ℃ で保たれ、定常状態となっている。カプセルの熱伝導率が 0.50 W/m・K、カプセルの厚さが 1.0 cm であるとき、球状カプセルが外部に放出する単位時間当たりの熱量はおよそいくらか。ただし，円周率を 3.14 とし、カプセルの熱伝導率は一定とする。

1． 1.3 × 10¹ W
2． 2.5 × 10¹ W
3． 1.2 × 10² W
4． 1.4 × 10² W
5． 2.8 × 10² W

 

 

 

 

 

　解 説　　　　　

「半径 r と 温度 T・・・で積分」とあるので、dr,dT を両辺に分けてみます。

Qdr = -κAdT です。κ は定数、単位時間あたりに流れる 熱量 Q も一定です。A = 4πr² なので、A は 変数 r により変化します。変数分離、つまり r と dr が同じ側になるように式変形します。

Q/4πr² dr = -κdT です。
r の範囲は r₁ ~ r₂、T の範囲は T₁ ~ T₂ です。両辺積分して計算すると、以下のようになります。

π = 3.14、κ = 0.50、T₂ ー T₁ = 40、r₁r₂/(r₂ – r₁)= 0.011/0.01 = 1.1 （※ r については、単位を m に直しています。）を代入して計算すれば、Q ≒ 2.8 × 10² です。

以上より、正解は 5 です。