問 題
理想溶液に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。
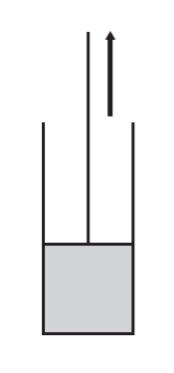
「温度 T、大気圧 P0 において、 2 種類の揮発性有機化合物A の液体(モル分率 xA、T における純粋な A の蒸気圧 PA)と揮発性有機化合物 B の液体(モル分率 xB =1 – xA)、T における純粋な B の蒸気圧 PB (≠PA))から成る理想溶液を図のようにピストンの付いた容器に満たした。
このピストンをゆっくり引き、溶液にかかっている圧力を減少させたところ、圧力がこの溶液と平衡にある気相の蒸気圧 Pg (<P0) に達したときに気相が現れ始めた。この蒸気圧 Pg は次式で表される。
Pg = ㋐
この気相における A のモル分率 yA を PA、PB、Pg で表すと
yA = ㋑ となる。」

解 説
2つ解法をあげます。
解法1:極端な例を考える、選択肢を活用する
XA = 1 とします。つまり、有機化合物 A のみです。この時、明らかに Pg = PA です。
選択肢 1 ~ 3 を正解と仮定すると、XA = 1 を代入した時、PA となります。一方、選択肢 4,5 が正解と仮定すると、XA = 1 を代入した時、2PB ー PA となります。よって、誤りです。従って、正解は 1 ~ 3 です。
次に、㋑ ですが
XA = 1 の時、A しかないのだから気相のモル分率は 1 です。Pg = PA を、選択肢 1 ~ 3 のそれぞれの式に代入します。選択肢 1 は「-1」、選択肢 2 は「0」、選択肢 3 は「1」です。
以上より、正解は 3 です。
解法2:ラウールの法則から計算する
ラウールの法則より
Pg = xAPA + (1 – xA)PB
= PB + (PA – PB)XA ・・・(1)従って、正解は 1 ~ 3 です。
全圧が xAPA + (1 – xA)PB で、A の分圧が xAPA なので
モル分率 yA =xAPA /{xAPA + (1 – xA)PB} です。
xA を 消去して、Pg で表せばよいので、(1)を xA について解いた xA = (Pg ー PB)/(PA – PB) を代入して整理すればOKです。先に 1-xA を計算しておきます。1 を通分すると (PA – PB)/(PA – PB) なので、1-xA = (PA – Pg)/(PA – PB) となります。
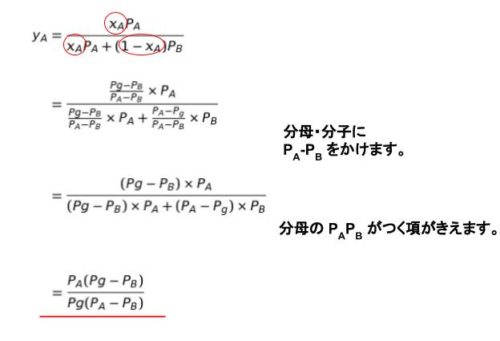
以上のような計算の結果、正解は 3 です。

コメント