国家公務員総合職（化学・生物・薬学）H30年 問19解説

　問 題　　　　　

ある二次反応の速度定数 k を測定したところ、600 K では、0.500 mol^-1・L・s^-1、624 K では、1.36 mol^-1・L・s^-1 であった。この反応の活性化エネルギーはおよそいくらか。ただし、自然対数の底 e を 2.72、気体定数 R を 8.31 J・mol^-1・K^-1 とし、また、k は次のアレニウス式に従うものとする。

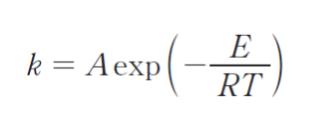
ここで，A は頻度因子、E は活性化エネルギー、T は絶対温度である。

1． 60   kJ・mol^-1
2． 130 kJ・mol^-1
3． 200 kJ・mol^-1
4． 270 kJ・mol^-1
5． 340 kJ・mol^-1

 

 

 

 

 

　解 説　　　　　

600K の時 0.5、624K の時 1.36 なので
0.5 = Ae^(-E/600R)
1.36 = Ae^(-E/624R) となります。

上の式を A について解くと A = 0.5/e^(-E/600R) です。これを下に代入します。

1.36 = 0.5/e^(-E/600R) × e^(-E/624R)です。
0.5 が邪魔なので 両辺 2 倍し、掛け算の形になおす（分母・分子に e^(E/600R)をかける）と

2.72 = e^(-E/624R) × e^(E/600R) です。左辺が ちょうど e¹ であることに注目します。

右辺の指数部分のみを見れば (E/R) × (1/600ー1/624) となります。これがちょうど 1 となればよいというわけです。

1/600 ー 1/624
= 1/(6 × 4 × 25) ー1/(6 × 4 × 26) なので、通分して計算すれば
1/(6 × 4 × 25 × 26) となります。R を 8.3 とみなせば、 (E/R) × (1/600ー1/624) の分母部分は大体 156 × 8.3 × 100 ≒ 130 × 10³ です。全体で 1 なので、E ≒ 130 × 10³ とわかります。

以上より、正解は 2 です。