国家公務員総合職（化学・生物・薬学）H30年 問11解説

　問 題　　　　　

正 3000 角形の頂点の一つを P₁ とし、残りの頂点を P₁ から時計回りの順に P₂、P₃、…、P₃₀₀₀ とする。線分 P₈₄ P₁₄₉₄ と線分 P₉₅₇ P₂₃₂₁ のなす角 θ（0° ≦ θ ≦ 90°）はいくらか。

1． 75°
2． 78°
3． 81°
4． 84°
5． 87°

 

 

 

 

 

　解 説　　　　　

いきなり正 3000 角形を考えるとピンとこないので、頂点２つから考えていくとイメージしやすいと思います。

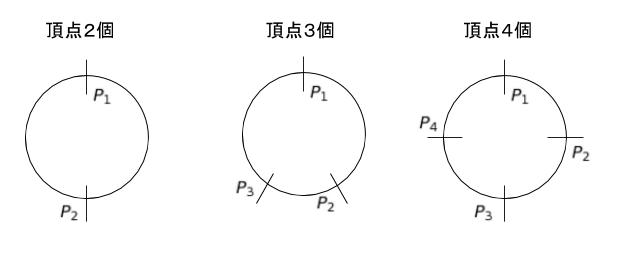
どこかを頂点 P₁ とおき、ちょうど真向かいに注目します。頂点が全部で２個の場合、P₂、頂点の数が奇数の場合は、ちょうど真向かいはなし。全部で４個の場合、P₃ となっています。頂点６個の場合を同様に考えると、真向かいは P₄ です。

規則性を考えれば「頂点の数÷2 + 1」が真向かいです。頂点 3000 個の場合、真向かいは P₁₅₀₁ となります。するとちょうど 4 等分していけば P₁1,P₇₅₁,P₁₅₀₁,P₂₂₅₁ とわかります。これを目安として、求めたい所を図示すると、下図のようになります。

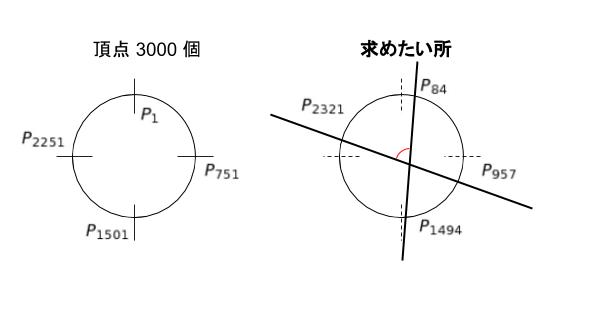
円に適当な 2 本の線分を引いて、交わった所の角を求めるので、以下のように補助線を引き、円周角の和を考えればよいです。

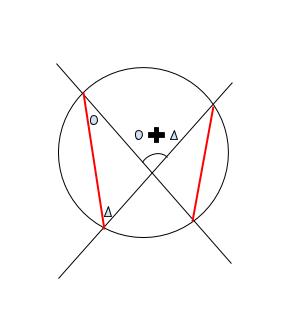
頂点の添字の差が ちょうど 1500 なら 円周角は 90° です。差が 1 なら 3/50 ° となります。P₉₅₇ ～ P₁₄₉₄ を弧とする円周角は 537 × 3/50 です。P₂₃₂₁ ~ P₈₄ までを弧とする円周角は 763 × 3/50 です。（「763」は、2321 ~ 3000 と 1 ~ 84 に分けて考えると求めやすいです。）

求める角度は 3 × (537 + 763)/50 = 78 です。

以上より、正解は 2 です。