国家公務員総合職（化学・生物・薬学）H29年 問17解説

　問 題　　　　　

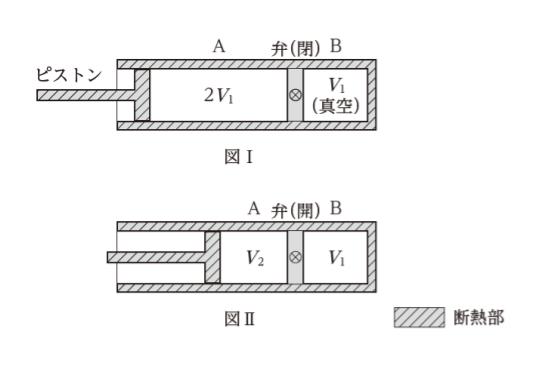
図Ⅰのように、断熱性の円筒形の容器が、熱をよく通す壁で二つの部屋 A（断熱性のピストンにより体積可変）及び部屋 B（体積 V₁）に仕切られている。この壁には小さな弁があり、弁を開くと A、B 間で気体が少しずつ移動し、閉めると遮断されるようになっている。

初め、A の体積は 2V₁ で、中に単原子分子の理想気体が入っており、A の圧力は外気圧に等しく、B は真空であった。この状態から、壁の弁を開いたところ、A の圧力は外気圧と等しい値を保ちながら、ピストンはゆっくりと移動し、図Ⅱのような熱力学的平衡状態となった。このときの A の体積 V₂ として最も妥当なのはどれか。ただし、円筒容器、壁、ピストンの熱容量は無視できるものとする。

なお、物質量 n の単原子分子の理想気体の内部エネルギー U は、気体定数を R、絶対温度を Tとして、U = 3nRT/2 である。

 

 

 

 

 

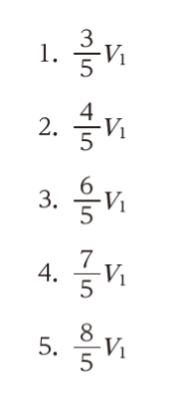
　解 説　　　　　

気体がされる仕事＝内部エネルギーの増加　です。「気体がされる仕事」＝ 外力が行う仕事です。仕事 ＝ 力 × 距離です。

「外力が行う」とは、本問において「ピストンが行う」です。ピストンがどれだけ移動したかを考えます。図Ⅰと図Ⅱを見比べて「3V₁ ー (V₁ + V₂)」＝ 2V₁ – V₂ が、ピストンが移動した距離です。従って、外力がした仕事は P × (2V₁ – V₂) です。

pv = nRT より、U = 3pV/2 です。内部エネルギーの増加分は、ΔU = 3pΔV/2　となります。気体の体積変化ですが、元々 2V₁ → V₁ + V₂ と変化しているため ΔU = 3p（V₁ + V₂) ー（２V₁）/2 = 3p(V₂ – V₁)/2 です。

よって
P × (2V₁ – V₂)  = 3p(V₂ – V₁)/2 です。
V₂ について解けば
V₂ = 7V₁/5 となります。

以上より、正解は 4 です。