国家公務員総合職（化学・生物・薬学）H28年 問11解説

　問 題　　　　　

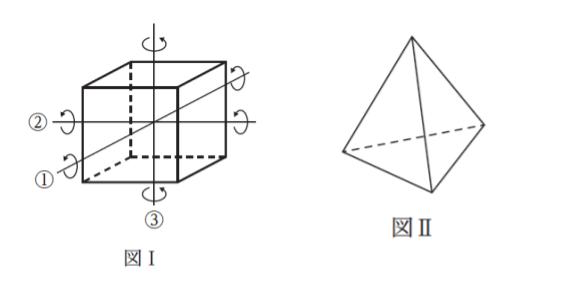
正六面体には、90° 回転させると元の正六面体に重ね合わせることができる回転軸が、図Ⅰのように 3 本存在する。ここで、図 Ⅱのような正四面体について考える。正四面体を 120°、180°回転させて元の正四面体に重ね合わせることができる回転軸の本数をそれぞれ N₁₂₀、N₁₈₀ とする。N₁₂₀ と N₁₈₀ の和はいくらか。

1． 4
2． 5
3． 6
4． 7
5． 8

 

 

 

 

 

　解 説　　　　　

知識として知らない場合は、図Ⅰをヒントとして考えることが期待されている問題かと思われます。

図Ⅰ ③ のパターンを、図Ⅱでも考えてみると「頂点とそれに向かい合う面の中心を通る軸」が対応すると考えられます。頂点が 4 つあるので、４本考えられます。これが N₁₂₀ です。

図Ⅰ ② のパターンを、図Ⅱでも考えてみると「相対する二辺の中点を結んだ軸」が対応します。辺が 6 本なので、軸は 3 本です。これが N₁₈₀ です。

図Ⅰ ① のパターンは、対称性が崩れるため、うまく元に重なりません。軸は合わせて 4 + 3 = 7 本です。

以上より、正解は 4 です。