問 題
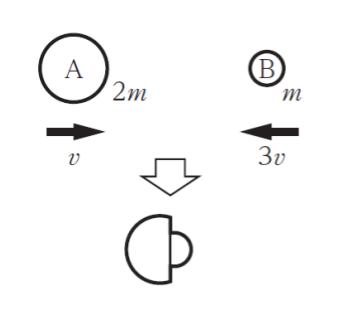
図のように、同一直線上を、質量 2m の物体 A が速さ v で、質量 m の物体 B が速さ 3v で進んでいる。これらがある点で衝突し、衝突後一体となって進んだ。衝突前に物体 A、B がもっていた運動エネルギーの和を E とすると、衝突後の物体がもっている運動エネルギーはいくらか。
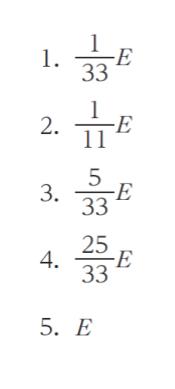
正解.1
解 説
運動量保存則を考えます。運動量は、質量 × 速さ です。
元々物質 A が、右向きに 2mv、物質 B が左向きに 3mv なので、衝突後は 左側に mv の運動量を有します。質量は一体となって 3m と考えられるため、速さ は v/3 です。
一方、衝突前に物体 A,B がもっていた運動エネルギーをそれぞれ KA、KB とおきます。運動エネルギーは mv2/2 です。従って、KA = mv2、KB = 9mv2/2 となります。和は 11mv2/2 です。これを E とおきます。
衝突後の物体の運動エネルギーは 1/2 × 3m × (v/3)2 = mv2/6 です。これは E/33 となります。
以上より、正解は 1 です。

コメント