導関数、微分

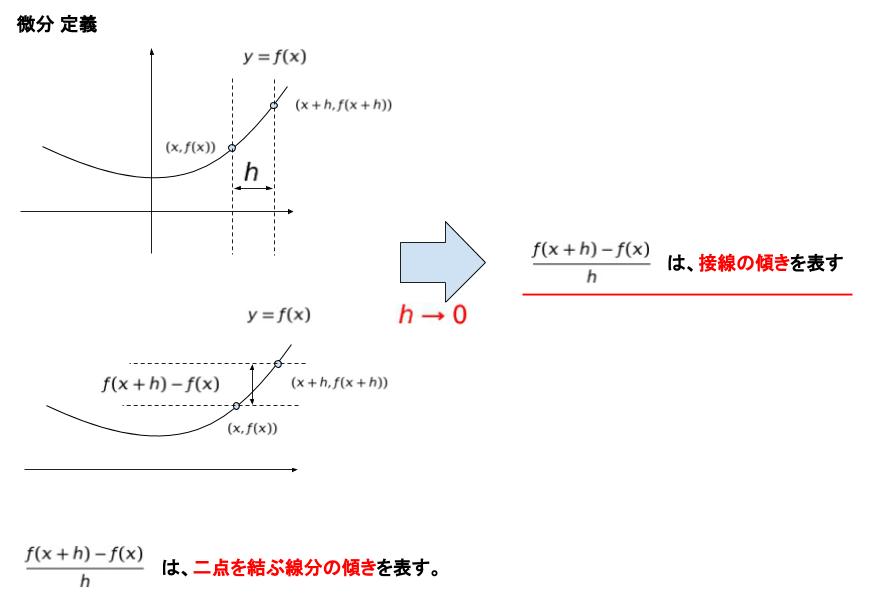
導関数とは、ある関数を微分して得られる関数のことです。微分するとは、ある関数を f(x) とする時、h → 0 の時の {f(x+h)ーf(x)}/h を求める　ということです。ある関数をグラフで表した時に、接線の傾きを求める計算といえます。イメージが下図になります。

代表的な関数の導関数について以下、例をあげます。冒頭であげた定義に基づいて計算する必要はなく、代表的な関数の導関数がどのように表されるかをおさえ、具体的に計算できれば十分です。y = f(x) の時、微分することを「y’」で表します。

代表的な関数の導関数（公式）
y = xⁿ → y’ = nx^n-1
y = sinx → y’ = cosx
y = cosx → y’ = -sinx
y = e^x → y’ = e^x
y = log_ex → y’ = 1/x

合成関数と積の微分について補足します。
代表的な関数の「x」の所に、別の式が代入された形の関数を 合成関数といいます。y = x² の x の所に sinx が入った y = (sinx)² が、合成関数の一例です。 このような合成関数の微分においては「入り込んだ式の微分」を掛ける必要があるという点を忘れないでください。

すなわち
y = (sinx)² であれば、y = x² のように見て y’ = 2sinx で終わりではない、ということです。入り込んだ式 sinx の微分が cosx なので、この cosx を掛けます。つまり y’ = 2sinx cosx が計算結果です。

積の微分（f(x)g(x) の微分）について
例として xsinx の微分について補足します。
f(x)g(x) の微分は「f(x)g(x)+f(x)g(x)」とまず書いて、「’」をそれぞれの項に振り分けてあげてください。すなわち「f'(x)g(x) + f(x)g'(x)」が求める積の微分です。

xsinx の微分であれば、とりあえず xsinx + xsinx って書いて、その後それぞれの項の片方を微分してあげてください。 x の微分は 1、sinx の微分は cosx なので、1sinx + xcosx です。1は省略できるので、sinx + xcosx が導関数です。

最後に
微分表記について補足します。
「変数が x である」ということを強調し、y’ を「dy/dx」と書くことがあります。y = 2x の時、dy/dx = 2 となります。