原始関数、不定積分、定積分

「微分したら 2x になる関数は？」
と聞かれたら、順に読んでいる人や微分に馴染みがある人はすぐ y = x² と頭に浮かぶと思います。定数があっても微分したら消えるから y = x² + C と定数項まで考えることもできます。微分したら f(x) になるような関数を F(x) で表し、原始関数と呼びます。y に対して Y で表すこともよくあります。

微分の逆演算を積分といいます。
例として、y = 2x を考えます。y = 2x に対し「微分すると 2x になるものなんだ？」という問に答える計算が積分です。積分するというのを ∫ dx という記号で式を挟んで表します。y = 2x に対し、y の原始関数を大文字 Y とすると Y = ∫ 2x dx と書きます。計算結果は x² + C です。定数部分が確定しないため不定積分といいます。C を積分定数と呼びます。計算結果を微分して元に戻ったら積分成功です。

代表的な関数の不定積分（公式）
y = xⁿ → Y =xⁿ⁺¹/n+1 + C  ※n ≠ -1
y = 1/x → Y = log_ex + C
y = sinx → Y = -cosx
y = cosx → Y = sinx
y = e^x → Y = e^x
y = log_ex → Y = xlog_ex – x + C

不定積分において
x の範囲を a ~ b と定めたものを定積分といいます。∫_a^b 2x dx のように表します。この定積分は 『x = a ~ b において、y = 2x と y = 0 の間の部分の面積』を表します。以下のようなイメージです。

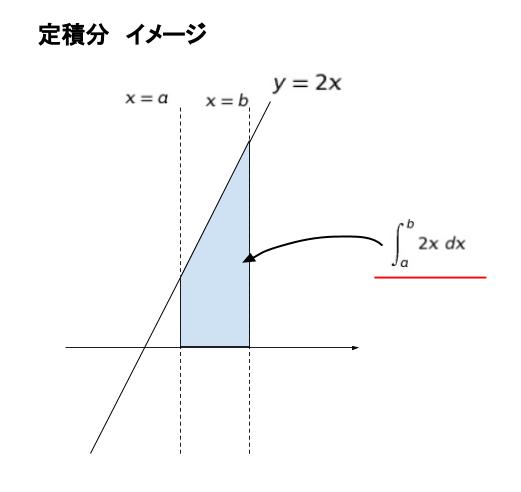
定積分の計算は
まず不定積分を行い、計算結果に a,b を代入します。それぞれ F(a) 、F(b) となります。F(b) ー F(a) が定積分の計算結果となります。数値の「上ー下」と意識するとよいです。先程の y = 2x について、x = 2~4 を考えてみましょう。まず不定積分は x² + C です。x = 2,4 をそれぞれ代入すると 4+C、16+C です。(16+C) – (4+C) = 12 となります。積分定数が消えて「答えが定まる」ので定積分です。そしてこの 12 が表しているのは、上図において a = 2 , b = 4 とした時の台形の面積です。