三角関数

三角関数は、三角比の関数です。
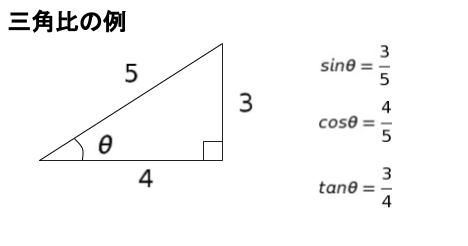
三角比とは直角三角形の辺の比です。三辺のうち二辺に注目した比なので 3 通りあります。それぞれ sin θ、cos θ、tan θ と表します。例として 長さ 3,4,5 の直角三角形に対して、最も小さな角を θ とすると、sin θ = 3/5、cos θ = 4/5、tan θ = 3/4 です。斜辺（r)の長さと sinθ、cosθ がわかれば、縦の長さ、横の長さをそれぞれ rsinθ、rcosθ で求めることができる点が重要です。

三角関数は
y = sin x や、y = cos x など、三角比の関数のことです。x の所には、1°、2°　といった角度ではなく『ラジアンを単位とする角度』がよく用いられます。π ラジアン = 180° です。※ π≒ 3.14 のため、1 ラジアン ≒ 57°　となります。

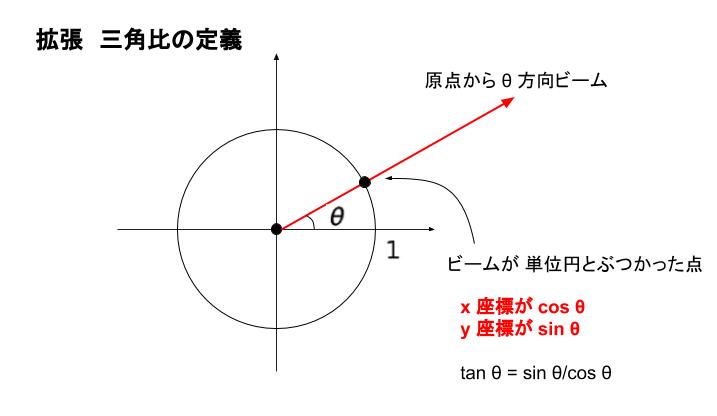
三角比が直角三角形の比なので、x の所には 0 ~ 90°（0 ~ π/2 ラジアン）までしか入らないように感じると思います。ここで三角比の定義の拡張を行うことで、x にはどんな数値も入るようにすることができます。半径 1 の円（単位円）を考え、原点から θ 方向にビームを発射すると円とぶつかります。この点の y 座標が sin θ、x 座標が cos θ とする　というのが、拡張した三角比の定義です。また、tan θ = sin θ/cos θ です。

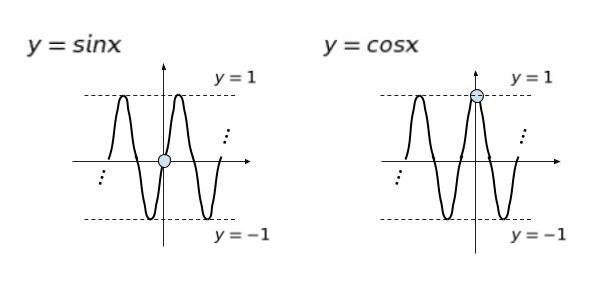
y = sinx、cosx、tanx は、定義からわかるように x = θ、θ + 2π、θ + 4π、、、の時に同じ値をとります。なぜかといえば、2 π = 360°なので、ぐるぐる回って結局ビームが同じ方向だからです。三角関数の最も大きな特徴は、周期性です。例えば波のような周期的現象を表せます。y = sin x、y = cos x についてグラフを以下に示します。