問 題
アセトアルデヒドの分解反応に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。ただし気体定数を 8.31J/(K・mol) とする。
「アセトアルデヒドの分解反応(CH3CHO → CH4 + CO)は
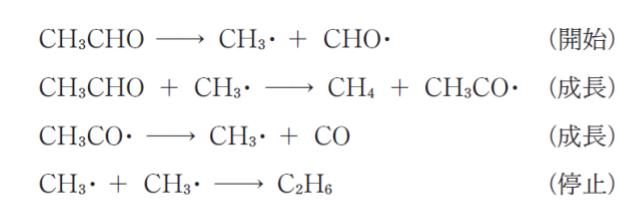
の機構で表される。
中間生成物の CH3CO・及び CH3・に定常状態近似を適用すると、反応速度は

と表される。
この分解反応を別の条件で行ったところ、反応は2次となった。2次反応を維持しつつ、700K 及び 1000K におけるみかけの反応速度定数 k2 を測定したところ、表のような結果となった。

この反応がアレニウスの式に従うとすると、反応のみかけの活性化エネルギーは ㋑ である。」

解 説
[CH3CO・]、[CH3・]に注目します。定常状態近似というのは、中間体の濃度が変わらないという仮定です。これにより、d[CH3CO・]/dt = 0、d[CH3・]/dt = 0 ということです。4つの素反応式の反応速度定数をそれぞれ k1,k2,k3,k4 とおくと、以下のような2式を作れます。
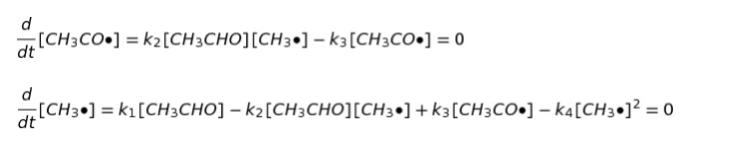
すごく複雑にみえるんですが、上の式の部分が下の部分にもあるので、下の式の右辺第2項、第3項が0になって消えます。従って、結局 k1 [CH3CHO] = k4[CH3・]2 ・・・(1)です。
アセトアルデヒドの分解反応として与えられた式は、成長段階の2式に展開されているため、2式における[CH3CHO]に注目し、式(1)の結果を利用すれば
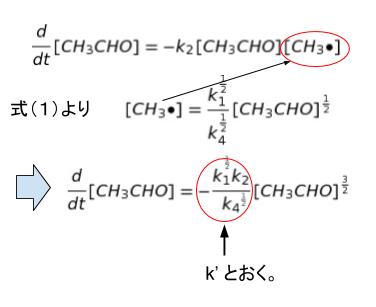
以上より、㋐ は 3/2 です。正解は 4 or 5 です。
㋑ ですが
アレニウスの式が lnk = -E/RT + lnA であることは知っている前提です。2つの温度における値を代入し、lnA を消去するために2式を引きます。
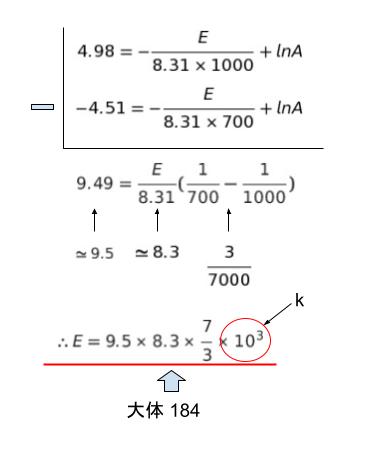
以上より、㋑ は 184 です。正解は 4 です。
参考)物理化学 4-1 6)

コメント