問 題
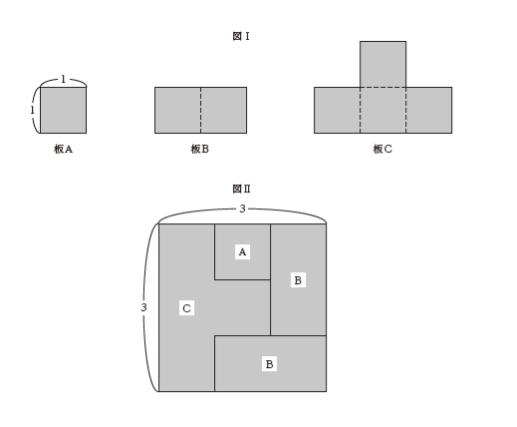
図Ⅰのような,一辺の長さが 1 の正方形の板A, 2 枚の板Aを一つにした板B, 4 枚の板Aを一つにした板Cの3 種類の板がある。これらの板を重ならないように置き,床を板で敷き詰めることを考える。
例えば,一辺の長さが3 の正方形の床は,図Ⅱのように,板Aを1 枚,板Bを2 枚,板Cを1枚使用して敷き詰めることができ,このときに使用した板の枚数は, 4 枚である。
一辺の長さが5 の正方形の床を,最も少ない枚数の板で敷き詰めるとき,板の枚数は何枚か。ただし,必ずしも3 種類の板全てを使用しなくてもよいものとする。
1. 7 枚
2. 8 枚
3. 9 枚
4. 10 枚
5. 11 枚
正解 (2)
解 説
一辺 5 の正方形なので、面積は 25 です。面積は板 C が一番大きいので、板 C をできるだけ敷き詰めて使ってみます。板 B,C の面積が 2,4 と偶数なので、板 A は1枚は使わなければならないはずです。
以下のように敷き詰めると、板 A も一枚なので、最小と考えられます。
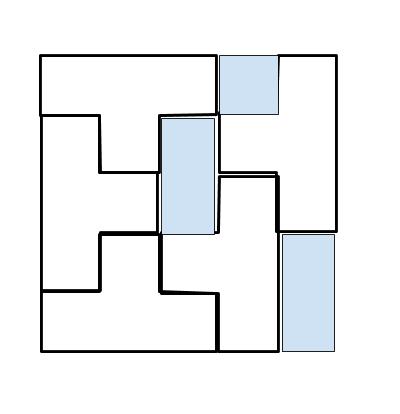
以上より、正解は 2 です。

コメント