問 題
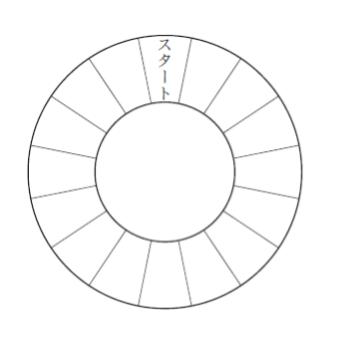
図のようにマスを配置する。コインと1~6の目をもつサイコロを同時に投げ、コインが表の場合はサイコロの目の数だけ時計回りに1マスずつコマを進め、コインが裏の場合はサイコロの目の数だけ反時計回りに1マスずつコマを進める。
2回投げ終わったときスタートした地点にいる確率として正しいのはどれか。
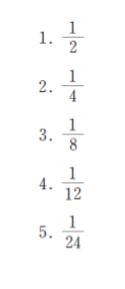
正解 (4)
解 説
まず具体的に考えると、イメージしやすいと思います。コインとサイコロを同時に投げ、1回め、2回め共に「表、1」が出たとします。すると、時計回りに1マスずつ、2回進みます。
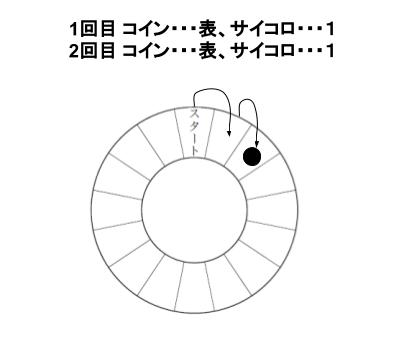
時計回りに1週するには、16 マス進む必要があります。サイコロ2回では、最高 12 マスしか進めません。従って「2回投げ終わった時、スタート地点にいる」のは「コインは表、裏が1回ずつ」、「サイコロの目は同じ」場合と考えられます。
コインが表、裏と出る確率は 1/2 です。
サイコロを振って、1回目と同じ目が2回目に出る確率は 1/6 です。つまり、求める確率は 1/2 × 1/6 = 1/12 です。
以上より、正解は 4 です。

コメント