問 題
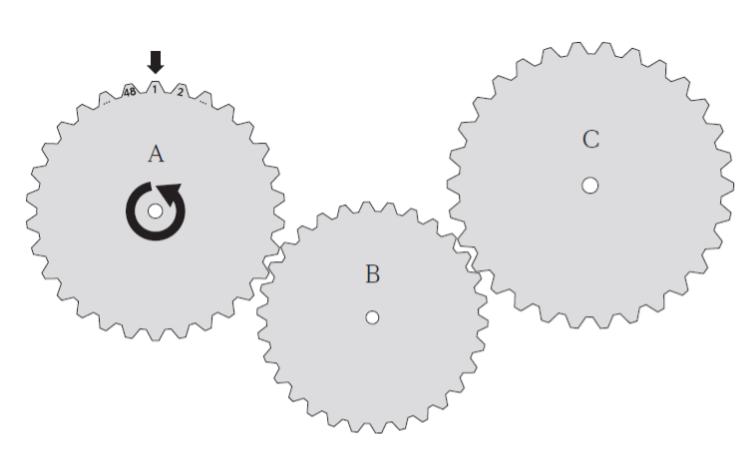
図は,歯が一つずつ噛み合いながらそれぞれ一方向にのみ回転する三種類の歯車を示す模式図である。歯車Aの歯数は 48 であり,それぞれの歯には 1 から 48 までの番号が時計回りに順に振られているが,歯車B及び歯車Cの歯数は不明である。また,歯車Aは反時計回りにのみ回転する。
次のことが分かっているとき,歯車Aがちょうど 5 周する間に歯車Cが回転する角度はおよそいくらか。
○ 歯車Aが回転を始めたとき,図の矢印が指す位置には1 番の歯があった。
○ 歯車Bがちょうど 1 周する間に,歯車Aは 2 周した後 3 周目に入っており,矢印が指す位置には 5 番の歯があった。
○ 歯車Bがちょうど 3 周する間に,歯車Cはちょうど 5 周した。
1. 960°
2. 1080°
3. 1200°
4. 1320°
5. 1440°
解 説
A の 1 周分の歯数が 48 です。この歯車 A がちょうど 5 周すると、48 × 5 = 240 だけ歯が回ります。この時、C が何周するかという問題です。
2つ目の箇条書きから
B の 1 周分の歯数 =「A の2周分+4」とわかります。48 × 2 + 4 = 100 です。
3つ目の箇条書きに注目します。
B が3周すると、歯数は、100 × 3 = 300 進みます。これで C が5周しているため、C の 1 周分の歯数は 60 です。歯数が全てわかりました。 A : 48、B : 100、C : 60 です。
A が5周すると、48 × 5 = 240 だけ歯が周ります。すると、C は 240 ÷ 60 = 4 周します。角度に直すと、1周が 360° なので、360 × 4 = 1440 ° です。
以上より、正解は 5 です。

コメント