問 題
ソロー・モデルの枠組みで考える。t 期の産出量を Yt ,資本ストックを Kt ,労働人口を Lt として,マクロ的生産関数が

で与えられているとする。また,労働人口は 0.02 の成長率で増加する。一方,資本ストックは t
期の投資を It とすると

で示される。ここでは,資本減耗率はゼロであるとする。さらに,各期では財市場が均衡し,貯蓄
率を s として,
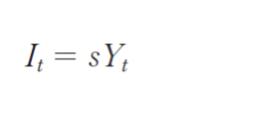
となり,この経済では,貯蓄率は一定で 0.4 であるとする。このとき,定常状態における労働人
口 1 人当たりの産出量はいくらか。
1. 10
2. 15
3. 20
4. 25
5. 30
解 説
ソロースワンモデルを考えます。成長率 ΔK/K = sy/k ー (d+n) ・・・(1)です。ここで s は貯蓄率、y が 1 人あたり生産(Y/L)、k が 1 人あたり資本(K/L)です。(2019 no40)。
定常状態において、ΔK/K = 0 です。従って、d + n = sy/k が成立します。資本消耗率 d = 0、自然成長率 n = 0.02、貯蓄率 s = 0.4 を代入すれば、0.02 = 0.4 × y/k です。すなわち、0.02 = 0.4 × (Y/L)/(K/L)・・・(1) と表すことができます。定常状態における労働人口 1 人当たりの産出量とは、(1) を満たす Y/L の値です。
以下、添字の t を省略します。
問題文の一番上の式より、Y = K1/2L1/2 です。両辺を L で割ります。すると、Y/L = (K/L)1/2 となります。 この変形は、ソロー・スワンモデルでの定石です。そして、両辺を 2 乗すれば (Y/L)2 = K/L です。(1)に代入すれば、0.02 = 0.4 × 1/(Y/L) となります。従って、Y/L = 20 です。
以上より、正解は 3 です。

コメント