問 題
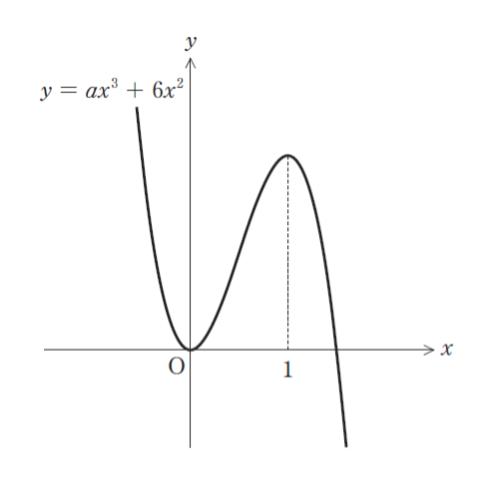
図のように、関数 y = ax3 + 6x2 が、x = 1 で極大値をとるとき、定数 a はいくらか。
1. -4
2. -2
3. -1
4. 2
5. 4
正解 (1)
解 説
【グラフに注目して a の符号決定】
図において、x < 0 の時、左に行くほどどんどん上に上がっています。これは例えば x = -100 の時に大きな正の値をとる、ということです。すると a の符号は明らかにマイナスです。このため、選択肢 4,5 は誤りです。微分について忘れていても、この検討はぜひ行えるようにしましょう!
【極値、極大値とは】
「極値」とは 「f ’ (x) が、その前後で符号が変わるような点における f (x) の値」です(参考 H28no6)。f ‘ (x) の符号が「+」から「ー」に変わる場合、極大値といいます。これは基礎知識です。
【定数 a を求める】
y ‘ = f ‘ (x) = 3ax2 + 12x・・・(1) です。「x = 1 で極大値をとる」のであれば、f ‘ (x) は x = 1 の前後で符号が変わります。そのため f ‘ (1) = 0 です。「極値を x = a でとる → f ‘ (a) = 0」という知識で処理しても OK です。
x = 1 を(1)に代入すると
f ‘ (1) = 3a + 12
3a + 12 = 0を解けば、a = – 4 です。
以上より、正解は 1 です。

コメント