2-コンパートメントモデルとは
人体を 2 つの四角い部屋に例えて薬物投与量と消失を考えるモデルです。1-コンパと比べて1つ増えるコンパートメントは、血中に薬物が投与され、分布し、平衡状態になるまで時間がかかるコンパートメントです。「末梢コンパートメント」 と呼ばれます。
抹消コンパートメントについて、具体的には
筋肉、脂肪、皮膚、骨など、ぱっと薬物が分布しない組織を1つの部屋にまとめたものと考えるとよいです。2-コンパートメントモデルのイメージは、以下の図になります。
【2-コンパートメントモデルのイメージ】
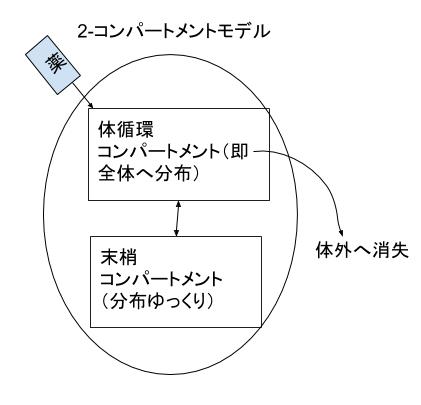
【2-コンパートメントモデルの 式やグラフ】
横軸に薬物投与後の時間(t)、縦軸に lnC を取ると
2-コンパートメントモデルで表される薬物動態は、以下のようなグラフになります。この際、縦軸として、C をとっても、ほぼ同じような形を示します。モデルにおけるどの部分の薬物濃度 C を見ているか、というと「体循環コンパートメント」です。
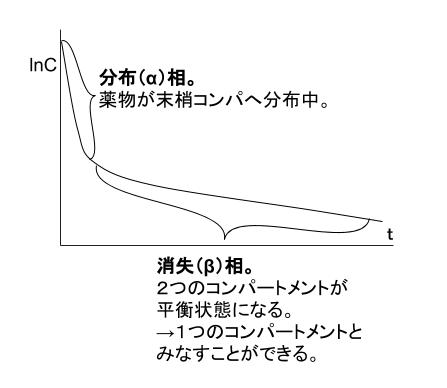
濃度と時間の関係を式で表すと
C = Ae-αt + Be-βt ・・・(1)です。
(1)の式 右辺における各項についてですが
抹消への分布のみに注目した式が 第1項の Ae-αt です。
体外への消失のみに注目した式が 第2項の Be-βt です。
ある程度時間が経過すると(消失(β)相)
一般的に α が大きいため、第1項が非常に小さくなり
式(1)は、C ≒ Be-βt で近似できます。
各項のみに注目してグラフで表すと
以下のようにまとめることができます。
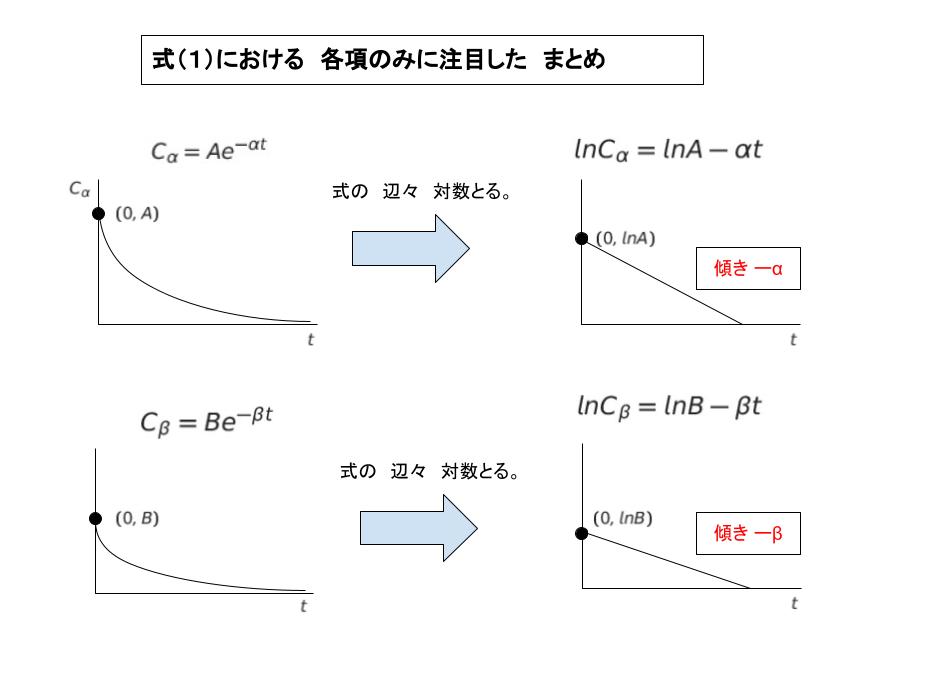
【パラメータ解析について】
未知の薬物を静脈投与し、TDM すると、初め急速に血中濃度が減少し、その後は緩やかに減少するデータがとれたので、2-コンパートメントモデルとみなし、血中濃度推移を式で表して解析するという状況を想像してみてください。
分布(α)相における血中濃度の減少は、抹消への分布だけでなく、体外への消失も反映しています。そのため、分布のみに関するパラメータ α をいきなり求めるのは、複雑な問題です。
そこで、パラメータを求める解析においては
まず十分時間がたった時の血中濃度に注目します。C ≒ Be-βt で近似できます。そこで、血中濃度の対数を数点求め、そこから直線を得ます。この直線の傾き から β を求めることができます。傾きと点の座標がわかっているため、B も簡単な計算で求めることができます。これで、式(1)における第2項が完全に求まりました。
次に、分布相における血中濃度の値に注目し、消失分を引きます。引いた値の対数をとることで、今度は A 及び、α を求めることができる、という流れになります。
以下は補足。
このように、2ーコンパートメントで表現される薬物は非常に多いようです。しかし、実際の臨床では、投与速度を遅くすることで投与直後の高い濃度を出さないようにしたうえで、遅い消失相を治療域の中心に入れるよう投与量を決定します。そうすれば結局1-コンパで必要な情報は解釈できることになるのです。以上補足。

コメント