Fischer投影式とNewman投影式

Fischer（フィッシャー）投影式

Fischer（フィッシャー）投影式とは、不斉炭素につく置換基の空間的な位置情報を残したまま、その構造式を二次元に書き表す方法です。

図1．破線-くさび形表記法（左）とFischer投影式（右）

図1の左側に示す化合物は、破線とくさび形の線を用いることで立体を表しています。それをそのままFischer投影式にすると、右側のようになります。つまりFischer投影式では、

• 水平の線：紙面手前側に伸びている結合
• 垂直の線：紙面の奥へ向かう結合

を表しています。

Newman（ニューマン）投影式

Newman（ニューマン）投影式は、立体配座を簡単に表記するために用いられる表記法です。

立体配座とは、単結合を回転させることでできる原子の空間的な位置の取り方のことです。この立体配座と分子の安定性の関係については、次項にて取り上げます。

話をNewman投影式に戻しますが、まずは具体例を見てください。

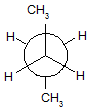
図2

これがブタンのNewman投影式です。元をたどると、以下のようになります。

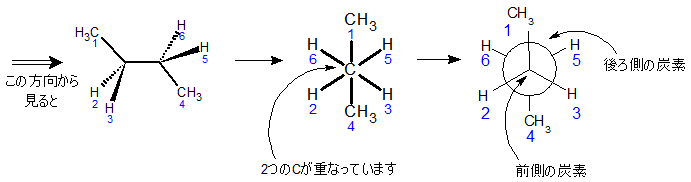
図3．Newman投影図の流れ

上図において、まず一番左はブタンの構造を表したものです。この分子を紙面左側から覗くとすると、手前の上側にメチル基（青字1）がきて、奥の下側にもメチル基（青字4）がきます。この状態が、ちょうど真ん中の図です。この真ん中の図をNewman投影図にしたものが右の図です。

矢印で示した中央の点が前面の炭素を表しており、そこからメチル基と水素2つ（青字1,2,3）が伸びています。また、円で示した部分が後方の炭素に該当し、そこからは青字4,5,6の原子（原子団）が結合していることがわかります。

有機反応においてこのNewman投影式を使うことはそう多くないのですが、分子の立体配座と安定性を考える際には非常に有用です。

次項では、エタンとブタンを例に取り、この投影式を使って立体配座の解説をします。