粉末X線回析測定法とは、粉末試料に X 線を照射し、回折した X 線を検出することにより、粉末の結晶がどのような構造をしているか、結晶の純度といった情報を取得することができる測定法です。
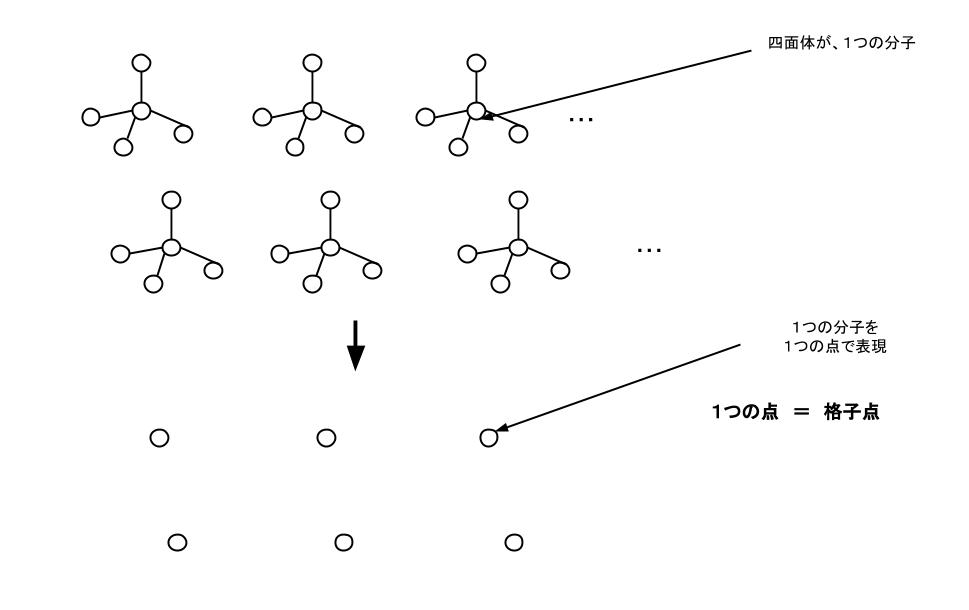
X 線回折測定法の原理の理解のために結晶格子について理解をする必要があります。結晶中の原子、又は分子を代表する点を格子点として表し、単位格子を3次元的に並べたものが空間格子です。イメージは下図のようになります。
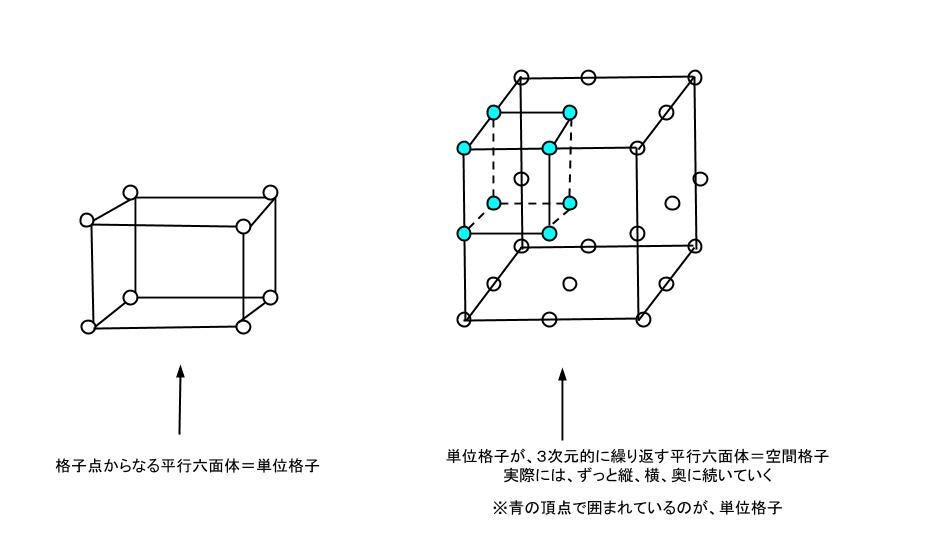
空間格子は、単位格子をなす、各辺の長さと、それぞれの辺のなす角により、7種の結晶系に分類されることが知られています。さらにそれぞれの結晶系においても分類がありあわせて14種類の格子(ブラベー格子)が知られています。参考) http://ja.wikipedia.org/wiki/%E7%B5%90%E6%99%B6%E6%A7%8B%E9%80%A0
空間格子は、平行した結晶面が連続していると見ることができます。結晶面の1例のイメージが下図になります。
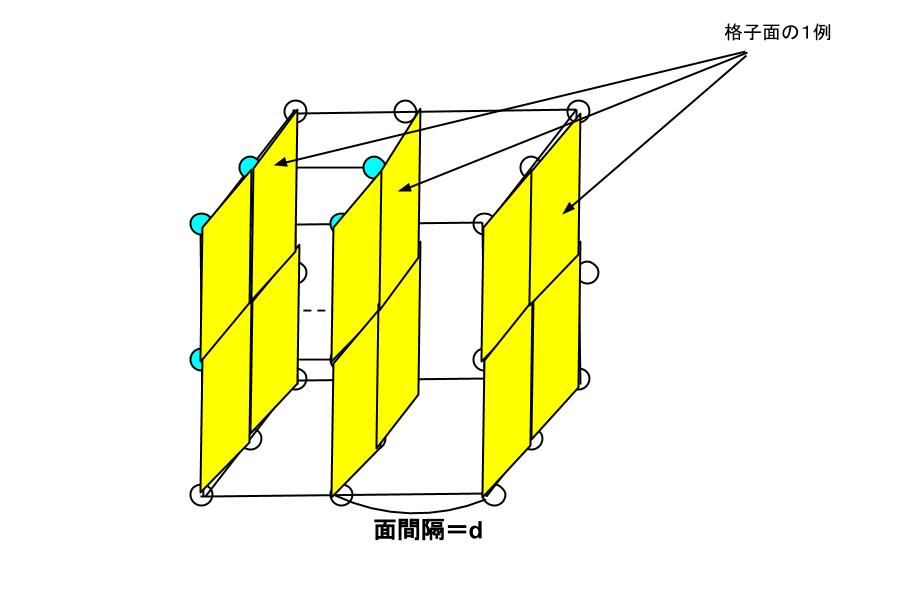
結晶面は、他にもいくつかの面を考えることができ、面を表現する方法として、ミラー指数が知られています。
ミラー指数とは、(100)といった表現をする数のことです。それぞれの数字の定義は「単位格子の1辺の長さ ÷ その方向の面間隔」です。それぞれの数字の求め方の具体例を以下に示します。単位格子のそれぞれの辺を、以下のように名づけます。
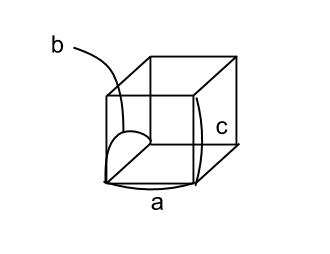
そして、どこかの面のどこかの点から、まず a 方向に向かって空間格子を突っ切ります。上の結晶例では、a 進むたびに、次の面にぶつかります。この時、1つめのミラー指数(1番左のミラー指数)は、a ÷ a = 1 です。
ミラー指数に、1はよく出る数値です。「a方向のミラー指数が1である」というのは「面を構成する辺に、a方向と平行であるものは存在しない」と読み替えてもよいです。
次に b 方向に進んでみると、いつまでたっても次の面にぶつかりません。この時、次の面にぶつかるまで∞(無限大)かかると考えます。ミラー指数(左から2番目のミラー指数)は、b ÷ ∞ = 0 です。
同様に c 方向に進んでも、いつまでたっても次の面にぶつかりません。やはり、次の面にぶつかるまで∞(無限大)かかると考えます。ミラー指数(左から3番目のミラー指数)は、c ÷ ∞ = 0 です。
よって、この面を表現するミラー指数は(100)となります。
さて、面間隔 d の結晶面に、入射角 θ で X 線が入射すると、それぞれの面で X 線が反射されます。この時、隣合う面から反射する光路差が波長の整数倍ならば、干渉効果により強めあいます。この結果が、干渉パターンという情報として得られます。このパターンが、空間格子のパターンを反映します。
この情報を解析することにより、粉末の結晶がどのような構造をしているかや、結晶の純度といった情報を取得することができるのです。利用法としては、結晶多形の評価などに用いられます。

コメント