国家公務員総合職（化学・生物・薬学）R3年 問23解説

　問 題　　　　　

球状分子の平均自由行程 λ は気体分子運動論より

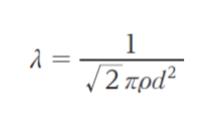
で表される。ここで、π は円周率、ρ は分子の数密度、d は分子の直径である。

ある理想気体が直径 0.30 nm の球状分子から成るとき、この分子の 410 K、1.0 × 10⁵ Pa における λ はおよそいくらか。ただし、π = 3.1、 √2 = 1.4、ボルツマン定数を 1.4 × 10^-23 J・K^-1 とする。

1． 4.5 × 10^-8 m
2． 1.5 × 10^-7 m
3． 4.5 × 10^-7 m
4． 1.5 × 10^-6 m
5． 4.5 × 10^-6 m

 

 

 

 

 

　解 説　　　　　

数密度 とは
ある体積 V に何個 分子があるかを表します。ρ = N/V…(1) です。

アボガドロ定数を N_A とおきます。
個数 N：物質量 × アボガドロ定数なので、N = n × N_A です。

(1) に代入すると
ρ = n × N_A/V…(2) と表すことができます。

理想気体の状態方程式 PV = nRT より
n/V = P/RT です。

(2) に代入すれば、ρ = P × N_A/RT です。ここで、ボルツマン定数 k = R/N_A なので ρ = P/kT と表せます。これで準備ができました。後は、問題文の式に数値代入して整理をすれば、大体 1.5 × 10^-7 m とわかります。以下、計算過程です。

以上より、正解は 2 です。

類題 H27no23 平均自由行程
https://yaku-tik.com/yakugaku/km-27-23/