問 題
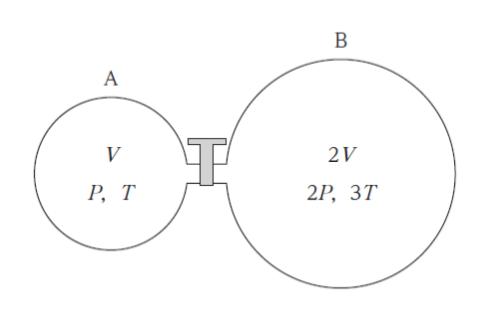
図のように、体積 V の容器 A 及び体積 2V の容器 B が、開閉できるコックの付いた細管で連結されている。コックが閉じた状態で、容器 A には圧力 P、絶対温度 T、容器 B には圧力 2P、絶対温度 3T の同種類の理想気体が封入されている。この状態からコックを開き、熱平衡の状態に達したとき、容器内の理想気体の圧力として最も妥当なのはどれか。
ただし、全ての容器及び細管は断熱材でできており、容器内の系において内部エネルギーは変化しない。また、容器の熱膨張及び細管の容積は無視できるものとする。
解 説
理想気体というキーワードがあるので、PV = nRT を思い出します。
本問は「温度の違う気体をコックで分離しておき、コックを開いて混ぜた時の圧力を求める」という状況が特殊です。状態方程式だけでは「コックを開いた時に T も P も変化してしまいわけがわからない」という問題があります。
そこで、理想気体に関するもう1つの重要な基礎知識である、気体の内部エネルギーに関する「U = (3/2) nRT」 を思い出して考えます。※この式は単原子分子についての式ですが特に指定がないので単原子分子と仮定して考えます。
コックが閉じた状態における
左側の容器の 気体内部エネルギーを U左とします。右側も同様に U右とおきます。
U左 = (3/2) nRT です。
PV = nRT より U左 = (3/2)PV…(1) と表せます。
U右 = (3/2) n’RT’ です。
(2P)(2V) = n’R(3T) より n’RT’ = 4PV より、U右 = (3/2) × 4PV = 6PV…(2) です。
コックを開いた時も内部エネルギーの合計は変わりません。
(1) + (2) = (15/2)PV です。
コックを開けた時の圧力を Popen とすれば、状態方程式より
Popen (3V) = n”RT” です。
状態方程式の 右辺 n”RT” は、内部エネルギーで表せます。
U = (3/2) nRT を変形すれば、nRT = (2/3)U です。
(2/3) × U
= (2/3) × (15/2) PV
= 5PV となります。
従って
Popen = 5PV/3V
= (5/3) P です。
以上より、正解は 2 です。
類題 国家一般職 化学 H29no11
https://yaku-tik.com/koumuin/h29-kagaku-11/

コメント