問 題
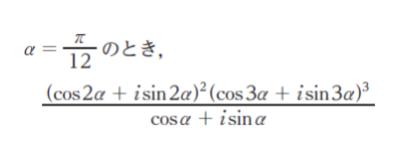
はいくらか。ただし,i を虚数単位とする。
正解.1
解 説
(cos θ + isin θ)n の形が見えるので ド・モアブルの定理 を思い出します。

まず、分子の ◯ 乗 部分を、ド・モアブルの定理で
(cos 4α + isin 4α)(cos 9α + isin 9α) となおせます。
それぞれの項を改めて (cos θ + isin θ)n の形になおせば
(cos α + isin α)4(cos α + isin α)9
=(cos α + isin α)13 と、分子をすっきりさせることができます。
与えられた式は
分子が (cos α + isin α)13
分母が cos α + isin α なので、約分すれば
(cos α + isin α)12 です。
ド・モアブルの定理で
cos 12α + isin 12α と表せます。
α = π/12 なので、12α = π です。π は 180° のことです。
cos 180° = -1、sin 180° = 0 は基礎知識です。
従って
求める値は -1 + 0 = -1 です。
以上より、正解は 1 です。
類題 R1 no1
https://yaku-tik.com/yakugaku/km-r1-01/

コメント
この問は,オイラーの公式e^{ix}=\cos x+i\sin xを用いると,
(e^{2iα})^2(e^{3iα})^3/e^{iα}=e^{12iα}=e^{iπ}=cosπ+i sinπ
が簡単に求められます.
仕事の式がw = – Fsとなってますが、移動距離と力の方向が同じとしていたらーは不要ではないでしょうか?