国家公務員総合職（化学・生物・薬学）R1年 問27解説

　問 題　　　　　

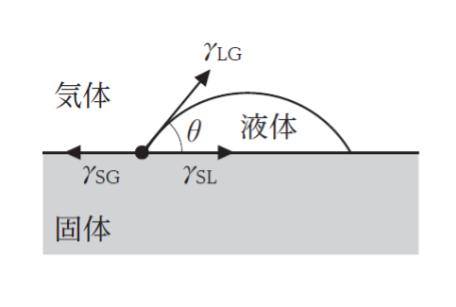
液体と固体が互いに離れた状態から液体が固体に付着し、その後、図のように液体と固体の接触線で力がつり合った状態で静止した。ここで、θ は接触角、γ_LG は液体の表面張力、γ_SG は固体の表面張力、γ_SL は固体と液体の界面張力である。

付着前後での自由エネルギー変化より、液体と固体を引き離すのに必要な単位面積当たりの仕事 W_A は、W_A =γ_LG + γ_SG – γ_SL となる。θ = 30°、γ_LG = 2.00 ×10^-2 N・m^-1 であるとき、W_A の値はおよそいくらか。

1． 3.00 × 10^-2 J・m^-2
2． 3.15 × 10^-2 J・m^-2
3． 3.41 × 10^-2 J・m^-2
4． 3.73 × 10^-2 J・m^-2
5． 4.00 × 10^-2 J・m^-2

 

 

 

 

 

　解 説　　　　　

力がつり合って静止　というのがポイントです。

横方向に注目すれば
γ_SG = γ_LG cos 30° + γ_SL です。

従って
W_A = γ_LG + γ_SG – γ_SL
= γ_LG + (γ_LG × √3/2 + γ_SL) – γ_SL
= (1+√3/2) γ_LG です。

γ_LG = 0.02 、√3 ≒ 1.73 なので
W_A = 0.02 + 0.0173 
≒ 3.73 × 10^-2 です。

以上より、正解は 4 です。