問 題
気体分子の運動に関する次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして最も妥当なのはどれか。
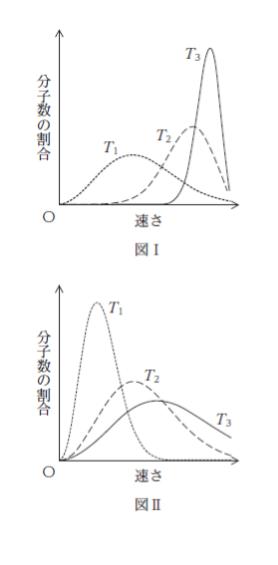
「気体分子の速さの分布は、マクスウェル・ボルツマン分布により表され、温度 T1、T2、T3( T1 < T2 < T3)に対して図 ㋐ のように変化する。
1.0 × 105 Pa、25 ℃ において、 窒素分子は、 平均約 ㋑ m・s-1 の速さで飛行し、平均自由行程約 100 nm で他の分子と衝突を繰り返す。ある 1 個の窒素分子に着目すると、毎秒約 5 × 109 回衝突する。温度一定の条件で、圧力を半分にすると、平均自由行程は ㋒ になる。」
㋐ ㋑ ㋒
1.Ⅰ 50 2 倍
2.Ⅰ 500 半分
3.Ⅱ 50 半分
4.Ⅱ 50 2 倍
5.Ⅱ 500 2 倍
解 説
㋐ ですが
温度が上がると速い分子の割合が多くなります。とはいえ、遅い分子がいなくなるわけではありません。図Ⅱが正しいと考えられます。正解は 3 ~ 5 です。
㋑ ですが
平均自由行程 = 平均の速さ/1個の分子についての衝突頻度 と表すことができます。そこから、平均の速さ=平均自由行程 × 衝突頻度なので、100 nm × 5 × 109 = 500 です。
ちなみに
分子が衝突を繰り返し、波の疎密が伝わっていく『音』の『音速』が 大体 25 ℃ならば 340m/s であることから、平均 3 桁程度の速度はあると大雑把に判断してもよいと思います。すなわち、50 か 500 かといえば 「500」 が妥当です。
㋒ ですが
圧力が半分なら、イメージとしてよりすかすかなので、衝突するまでの平均自由行程は「長くなる」と考えられます。2 倍か半分かといえば「2 倍」と考えられます。
以上より、正解は 5 です。

コメント