問 題
気体分子運動論に関する次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして最も妥当なのはどれか。
「・気体分子運動論は、気体分子間及び気体分子と容器の壁との間で起こる衝突は、㋐ であるという仮定に基づいている。
・体積 V の立方体に入っている質量 m の気体分子 N 個による圧力は ㋑ である。ここで
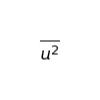
は気体分子の平均二乗速度である。
・気体定数を R、気体の絶対温度を T とすると、気体 1 mol の全運動エネルギーは 3RT/2
である。アボガドロ定数を NA とすると、気体分子の根平均二乗速度
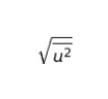
は ㋒ である。」

解 説
㋐ ですが
弾性衝突、つまり反発係数 e = 1 を仮定します。そうでないと、衝突を繰り返すたびにどんどん速度が小さくなってしまうからです。正解は 1 ~ 3 です。
㋑ ですが
まず、【1分子、1方向】で考えます。例として『横方向のみ、1分子の気体の運動』を考えます。一辺 L の立方体(体積 V = L3) 、気体の速度 vx とおきます。mvx の運動量を持っています。1回壁に衝突すると、完全弾性衝突なので、ーmvx に運動量が変化します。この時、力積は運動量の変化量なので、力積が 2mvx です。
【単位時間あたりに何回壁に衝突するのか】を考えます。
速度 vx で、距離 L の道を往復しているので、1 つの壁に注目すれば、1回衝突した後、気体分子が 2L 進むとまた衝突します。従って、単位時間あたり v/2L 回壁に衝突するとわかります。(例として、1 秒間に 4 m 進むとして、一辺 1 の立方体で一つの壁に注目すれば、1 秒に 2 回衝突です。)すると、1個の分子が単位時間あたりに壁に与える力積の合計は、2mvx × vx/2L です。
そして、力積 は F × t なので、単位時間あたりであれば、これが正に F、つまり気体が壁に与える力 です。圧力は「力÷面積」なので、L2 で割れば、2mvx2/2L3 = mvx2/V となります。分子は実際には N 個あるため、N をかけます。Nmvx2/V です。
また、平均速度 v を用いると、 v2 = vx2 +vy2 +vz2 です。x,y,z 方向に区別はないため、全ての項を vx2 としてかまいません。従って、vx2 = v2/3 です。これを代入すれば、 Nmv2/3V を得ます。
㋒ ですが
p = Nmv2/3v を、変形すればよいです。ここで pv = nRT を用います。さらに N/NA = n です。
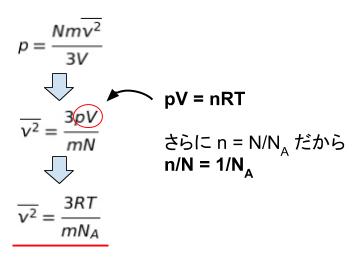
後は両辺 √ をとればよいです。
以上より、正解は 1 です。

コメント