問 題
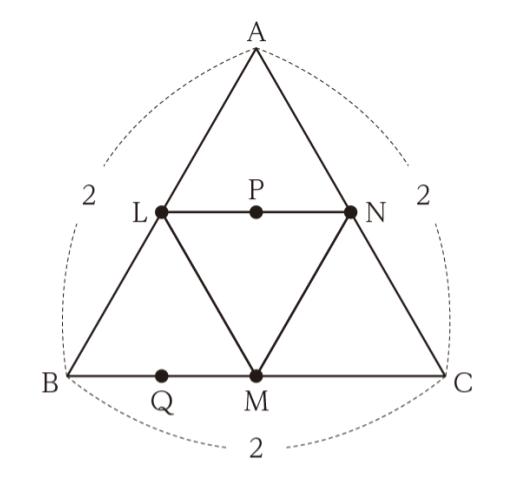
図のように、 1 辺の長さが 2 の正三角形 ABC の 3 辺 AB、BC、CA の中点をそれぞれ L、M、N とし、線分 NL、BM の中点をそれぞれ P、Q とする。線分 LM、MN、NL に沿って三角形を折り曲げ、正四面体を組み立てたとき、線分 PQ の長さとして正しいのはどれか。
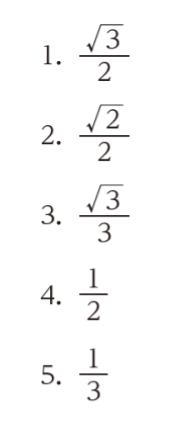
正解.2
解 説
一辺 1 の正四面体が組み立てられます。真上から見た図を考えるとわかりやすいのですが、求める PQ は、1 辺 1/2 の正方形の対角線です。
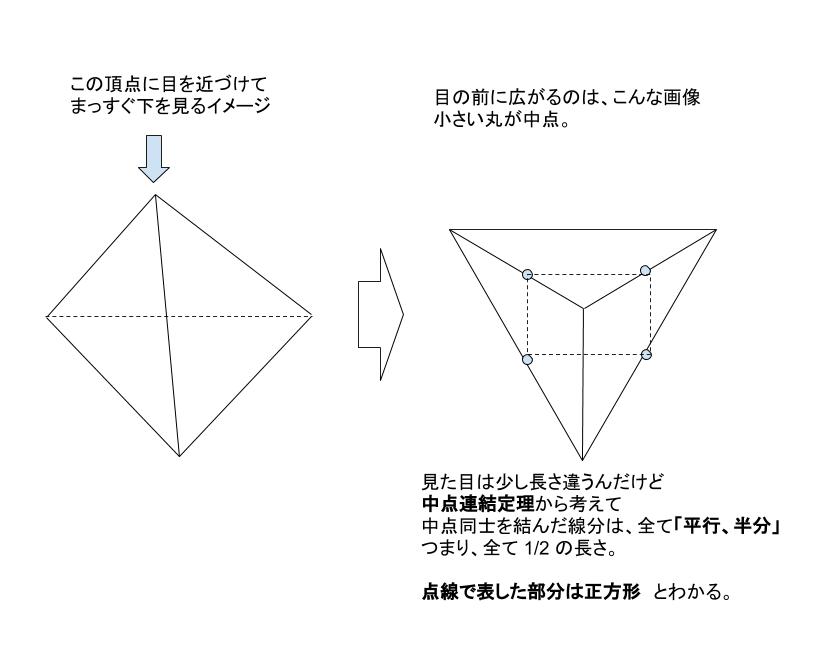
上図の右側において、P は底面三角形の辺における中点、Q は頂点から伸びる線分の中点です。 そして、Q から見て、頂点をはさんだ向こう側にいる方の点が P です。よって PQ が正方形の対角線に対応します。従って、PQ の長さは √2/2 です。
以上より、正解は 2 です。

コメント