国家公務員総合職（化学・生物・薬学）H28年 問23解説

　問 題　　　　　

ファンデルワールスの式に関する次の記述の㋐、㋑、㋒に当てはまるものの組合せとして最も妥当なのはどれか。

「実在気体の状態方程式の一つであるファンデルワールスの式は、a、b をファンデルワールス係数として、圧力 p、モル体積 Vm、温度 T、気体定数 R について

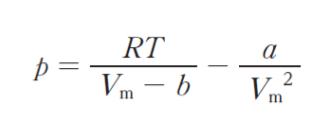
と表される。また，臨界点における圧力 p_c，モル体積 Vc，温度 Tc は，臨界点が pV 曲線の変曲点であることから，それぞれファンデルワールス係数と関連付けられる。ここで，換算変数 pr = p/p_c、Vr = Vm/Vc、Tr = T/Tc を導入すると，ファンデルワールスの式は物質固有の定数を含まない形として表され、pr、Vr、Tr について

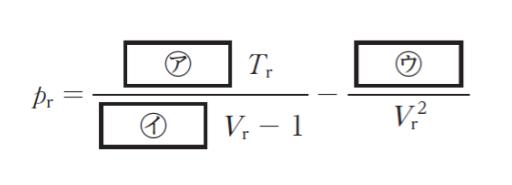
と表すことができる。」

㋐　㋑　㋒
1． 3 　3 　8
2． 3 　8 　3
3． 3 　8 　8
4． 8 　3 　3
5． 8 　3 　8

 

 

 

 

 

　解 説　　　　　

「臨界点が pV 曲線の変曲点」とあるので、微分した式 、及び二回微分した式に 圧力 p_c 、体積 Vc、温度 Tc を代入すれば、0 です。dP/dv = 0、d²P/dV² = 0 を計算します。また、臨界点における圧力が p_c 、体積が Vc、温度が Tc なので、ファンデルワールスの式にそのまま代入した式も考えます。

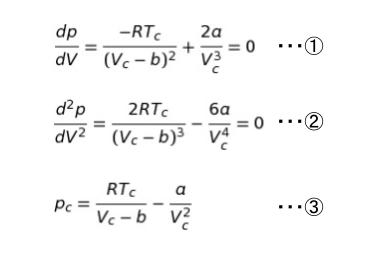
pc 、 Vc、Tc　について 3 つ式ができたため、解けます。

① に 1/(Vc – b) をかけて、② の第一項に代入して整理すれば、Vc = 3b です。

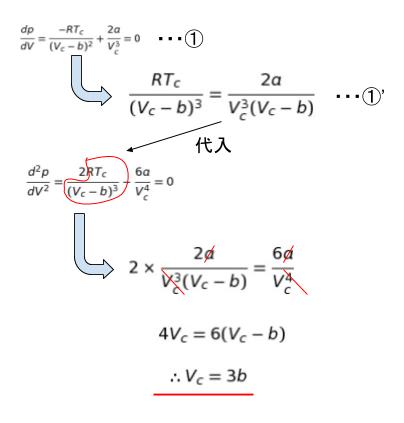
Vc = 3b を、式 ① に代入して整理すれば、Tc = 8a/27Rb です。

Vc = 3b、Tc = 8a/27Rb を 式 ③ に代入すれば、p_c = a/27b² です。

換算係数から「p = p_cp_r、Vm = VcVr、T = TcTr」です。もとのファンデルワールスの式に代入し、さらに Vc = 3b、Tc = 8a/27Rb 、p_c = a/27b² すれば、以下のように p_r = 8Tr/(3Vr – 1)-3/Vr² となります。

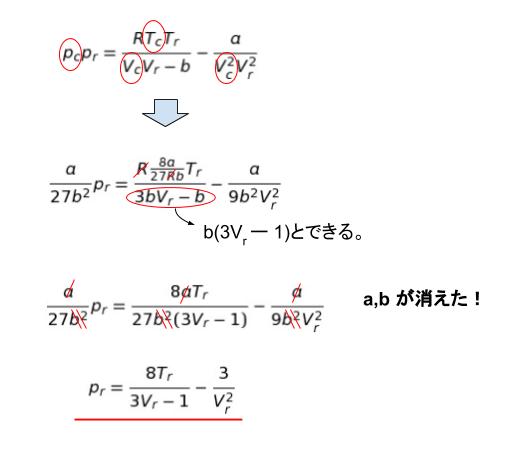
以上より、正解は 4 です。