問 題

シクロヘキサンの各温度における状態及び蒸気圧は表のとおりである。この値から求まるシクロヘキサンの三重点温度 Ttrip に関する次の記述の ㋐、㋑、㋒ に当てはまるものの組合せとして最も妥当なのはどれか。ただし、気体定数 R を8.31 J・mol-1・K-1 とする。
「液体とその蒸気が平衡状態にある場合、蒸気圧 P と温度 T には、モル蒸発熱を Δvaph とし、液体のモル体積が気体のモル体積より十分小さく無視できるとすると、クラウジウス・クラペイロンの式から
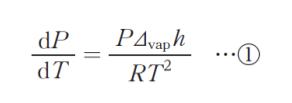
の関係が成り立つ。また,Δvaph の代わりにモル昇華熱 Δsubh を用いたものは,固体とその蒸気が平衡状態にあるときの関係を表す。表の温度範囲においてシクロヘキサンの Δvaph,Δsubh が変化しないものとした場合,式①を固体のシクロヘキサンに適用すると,シクロヘキサンのΔsubh は,㋐ kJ・mol-1 と計算される。さらに,固体 ⇆ 気体の蒸気圧 Psg とT の関係は,
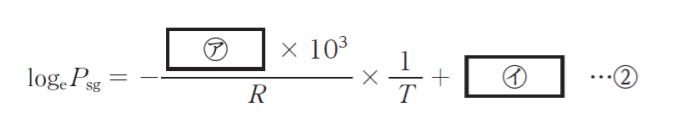
となる。同様に,液体 ⇆ 気体の蒸気圧 Plg は
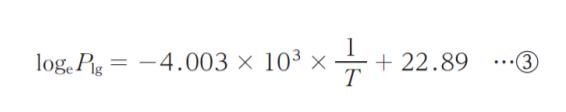
となる。式 ②,式 ③ から Ttrip を求めると,Ttrip = ㋒K となる。」
㋐ ㋑ ㋒
1. 36.5 24.3 270
2. 36.5 24.3 282
3. 36.5 26.3 270
4. 75.6 26.3 270
5. 75.6 28.2 282
解 説
㋐ ですが
lnP = -ΔH/R × (1/T) + C を使って計算します。(微分方程式を解いてもよいのですが、これは覚えておいた方が便利です。)
1/T,lnP を、表の数値を利用してまとめると、以下のようになります。

縦軸を logeP、横軸を 1/T としたグラフの傾きが -ΔH/R です。従って、傾きに R = 8.31 をかければ、ΔH の大きさがわかります。
1/T が 0.1589 × 10-3 増えると、logeP が 0.6931 減っています。従って、傾きは 0.6931/(0.1589 × 10-3) = 0.6931 × 103/0.1589 です。大体 4.5 × 103 ぐらいと評価できます。
103 は、㋐ の単位が kJ なので、無視します。
4.5 に R = 8.31 をかけるので、選択肢より 36.5 の方が妥当と判断できます。 正解は 1 ~ 3 です。
次に ㋑ ですが
logeP を y、1/T を X とおけば
y = -36.5/8.31 × 「103 × X」 + ㋑ です。103 は、単位の 「k」をなおしたものです。すると「103 × X」の部分は、正に 1000/T なので、表の値をそのまま代入すればよいです。例えば、y に 7.883、X に 3.7286 を代入すれば、㋑ を求めることができます。
7.883 = -4.5 × 3.7286 + ㋑ とみれば、大体 8 = -16,… + ㋑ です。(参考:4.5 × 3.7 = 16.65)選択肢より、㋑ は 24.3 と考えられます。正解は 1 or 2 です。
㋒ ですが
三重点において、②、③ が等しくなるため、以下の式が成り立ちます。
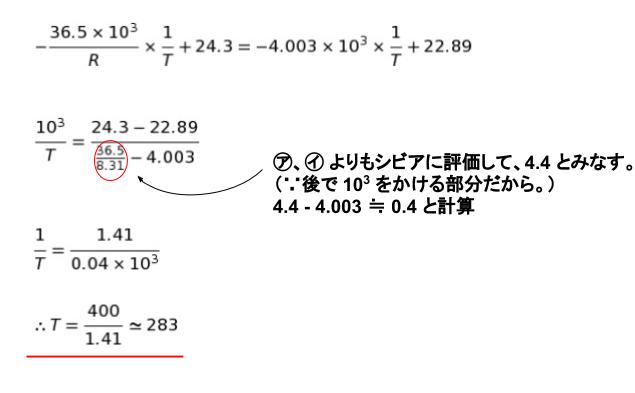
㋒ は選択肢から 282 が妥当と考えられます。
以上より、正解は 2 です。

コメント