問 題
気体 N2O4 は、解離反応を起こし、 2 分子の気体 NO2 となる。1 mol の N2O4 を密閉
容器に入れ、標準圧力(1.00 × 105 Pa)の下で、ある温度T〔K〕に保ったところ、N2O4 の解離度 a で、解離平衡に達した。T における N2O4 及び NO2 の標準生成ギブズエネルギーをそれぞれ 98.20 kJ・mol-1、51.59 kJ・mol-1 とすると、a2 はおよそいくらか。ただし、気体定数 R とT の積を 2.49 kJ・mol-1、自然対数の底 e を2.72 とする。
1. 0.0035
2. 0.014
3. 0.020
4. 0.033
5. 0.16
解 説
圧平衡定数を K とおきます。N2O4 ⇆ 2NO2 です。反応開始時、平衡時 の それぞれの気体の物質量についてまとめると、以下の表のようになります。
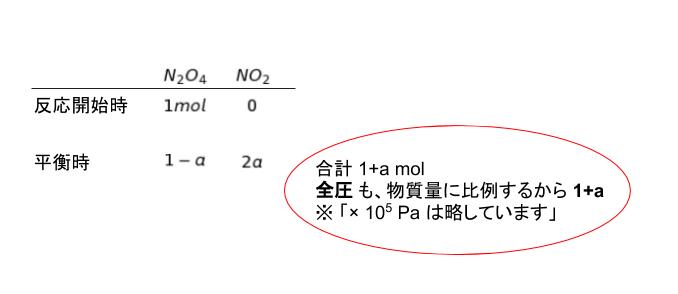
圧平衡定数 Kp = [NO2 の分圧]2/[N2O4 の分圧] です。それぞれの分圧は 分母が 1-a/1+a、2a/1+a と表されます。計算すると、Kp = 4a2/1-a2 となります。問われているのが a2 なので、a2 について解くと、a2 = Kp/4+Kp ・・・(1)と表すことができます。後は圧平衡定数がわかればいいと考えられます。
問題文から、それぞれの標準生成ギブスエネルギーがわかっています。ΔG = -RT lnK を思い出します。標準生成ギブスエネルギーなので、右辺の K が圧平衡定数 Kp です。
ΔG は、2 × 51.59 – 98.20 = 4.98 です。ちょうど RT の積の 2 倍になっていることから、問題文で与えられた数値の使い方として、きっと間違っていないと実感できるのではないでしょうか。
4.98 = -2.49 lnKp となるので、lnKp = -2 です。∴ Kp = e-2 です。問題文より、e = 2.72 として、式 (1) に代入すると
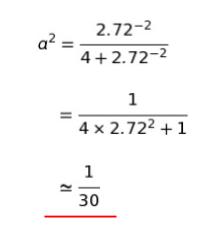
以上より、正解は 4 です。

コメント