問 題
x は t の関数であり、微分方程式
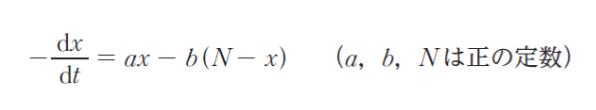
及び初期値 x(0) = N を満たす。このとき
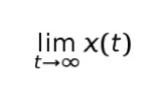
として最も妥当なのはどれか。
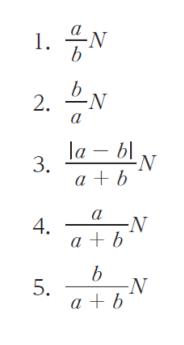
正解.5
解 説
具体的に考えます。
まず
ーdx/dt = (a+b)x -bN ・・・(1) と変形します。
するとこの式は「x を t で微分すると、x の定数倍に定数を加えたもの」と読み変えることができます。『微分したのに定数倍』ということから ect を項に含むと考えます。※ c は定数です。
ひとまず、x = ect とおいてみます。-dx/dt = -cect となります。(1) の右辺と比較すると a+b = -c かつ、-bN = 0 となります。しかし b,N は共に正の定数なので、これを満たす b,N は見つかりません。
そこで、x = ect + d とおきます。-dx/dt = -cect という微分した結果は変わりません。(1) の右辺を見ると (a+b)(ect + d) -bN です。展開すると (a+b)ect +d(a+b) -bN です。係数を比較すれば a+b = -c です。これを代入して定数項を係数比較すれば -cd -bN = 0 ・・・(2)となります。
求めたいのは、x(t) の t が無限大にとんだ時の値でした。まず a+b = -c なので c = -(a+b) です。a,b は正なので、c は負となります。これにより ect の部分は t が無限大の時 0 に収束するとわかります。残るのは d です。
(2)の式を d について解けば d = ーbN/c です。そして、c = -(a+b) でした。代入すれば d = bN/(a+b) です。これが求める極限です。
以上より、正解は 5 です。

コメント