問 題
図のように、水平で滑らかな床に質量 mA、mB の小球 A、B を置き、ばね定数 k の軽いばねでつなぎ、静止させた。ある瞬間に、 A に右向きの速度を与えたところ、この系の重心から見てA 、B はそれぞれ単振動した。重心から見た B の単振動の周期として最も妥当なのはどれか。
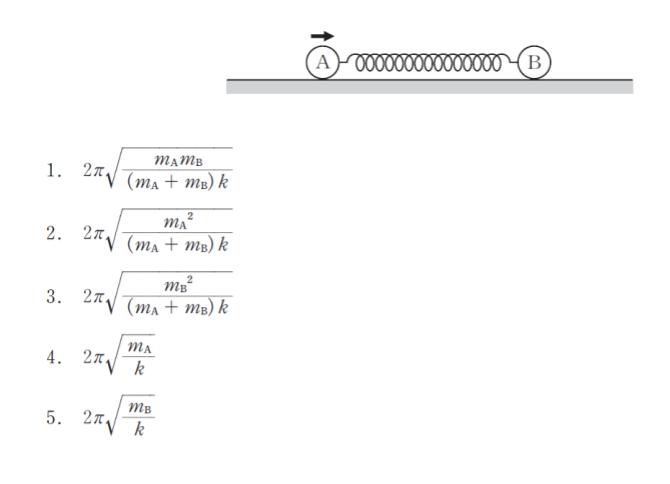
正解.1
解 説
単振動の周期なので
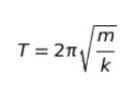
を思い出します。
自然長 L として、重心の x 座標を 0 とします。 B の x 座標は mA/(mA + mB) × L です。ばねの長さと、ばね定数は反比例します。重心から見た B までのばねのばね定数を k’ とおきます。長さが L でばね定数が k なので、長さが mA/(mA + mB) × L になったのであれば、k’ = (mA + mB)/mA × k です。これを公式に代入すれば
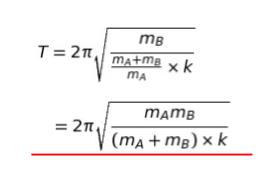
以上より、正解は 1 です。
別解
極端な例として、mA = 0 及び mB = 0 の時、周期も何もないはずなので、0になると考えられます。少なくとも、まともな値が出てはいけません。よって、まず選択肢 4,5 は明らかに誤りです。mB = 0 の時、選択肢 4 は普通の値になります。mA = 0 の時、選択肢 5 は普通の値になります。
同様に、mB = 0 の時、選択肢 2 は 2 π√mA/k となり、普通の値になります。mA = 0 の時、選択肢 3 は 2 π√mB/k となり、普通の値になります。よって、選択肢 2,3 も誤りです。
以上より、正解は 1 です。

コメント