国家公務員総合職（化学・生物・薬学）H27年 問2解説

　問 題　　　　　

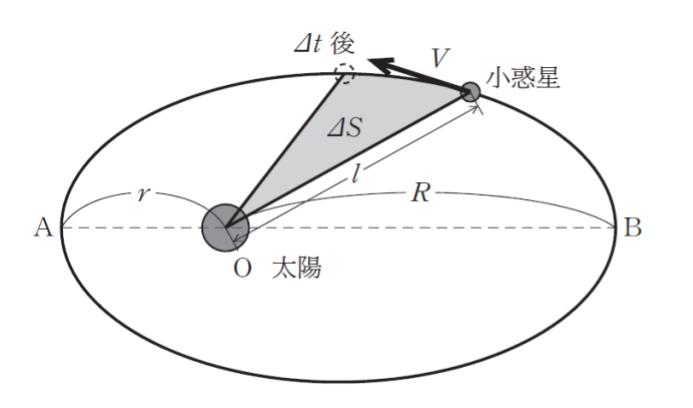
図のように質量 M の太陽の周りの楕円軌道上を運動する小惑星の点 B における速さとして最も妥当なのはどれか。

ただし AB は楕円の長軸であり太陽の中心 O から点 A、B までの距離をそれぞれ r、R (r ≠ R) とし、万有引力定数を G とする。また小惑星の中心と太陽の中心までの距離が l のときの小惑星の速さを V、小惑星の質量を m とすると力学的エネルギー

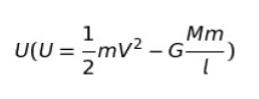
は保存されており、時間 Δt に小惑星と太陽を結ぶ線分が通過する面積 ΔSについて、ΔS/Δt は常に一定である。

 

 

 

 

 

　解 説　　　　　

点 A における速さを v、点 B における速さを V とおきます。面積一定の法則から、点 A、点B における通過面積を三角形と考えて、rv/2 = RV/2 が成立すると考えられます。ここから V = (r/R) × v ・・・（１）です。

次に、点 A,B における力学的エネルギー保存則より

式（１）の両辺を２乗して、V² = ・・・としておき、力学的エネルギー保存則から導いた式を代入して V について整理します。

以上より、正解は 2 です。