問 題
ベンゼンの6員環の六つの炭素原子について、ある炭素原子を炭素1とし、時計回りに炭素2、 炭素3、 … 炭素6とする。φk を k に対応する番号の炭素原子の 2pz 原子軌道(z はベン
ゼン環を含む平面に垂直な座標軸)とすると、ベンゼンの6員環に非局在化した分子軌道の波動
関数 Ψn (n = 1~ 6) は、ヒュッケル近似のもとで、次のように表すことができる。このとき、Ψ2 と同じエネルギーをもつ分子軌道の波動関数はどれか。
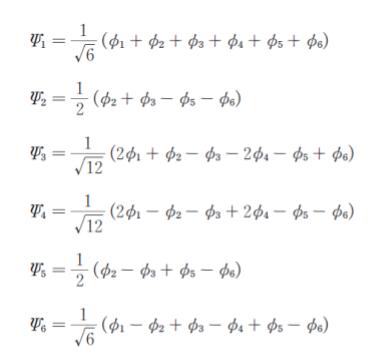
1. Ψ1
2. Ψ3
3. Ψ4
4. Ψ5
5. Ψ6
正解.2
解 説
「分子軌道の波動関数」は、「構成原子の原子軌道を表す波動関数」の「線形結合(ax+by+・・・の形)」で表すことができます。Π 分子軌道の波動関数 Ψ = c1φ+c2φ+c3φ+c4φ+c5φ+c6φ とおけるということです。 符号が「+」なのか「ー」なのかだけに注目すると、まず Ψ1 は以下のように表すことができます。
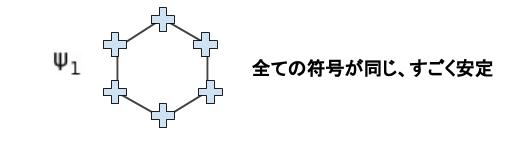
※軌道の符号が同じ同士がとなりあうと「結合性分子軌道」で「安定」と読みます。符号が逆は「反結合性分子軌道」で「不安定」と読みます。
Ψ2 ~ Ψ6 を同様に表すと以下のようになります。
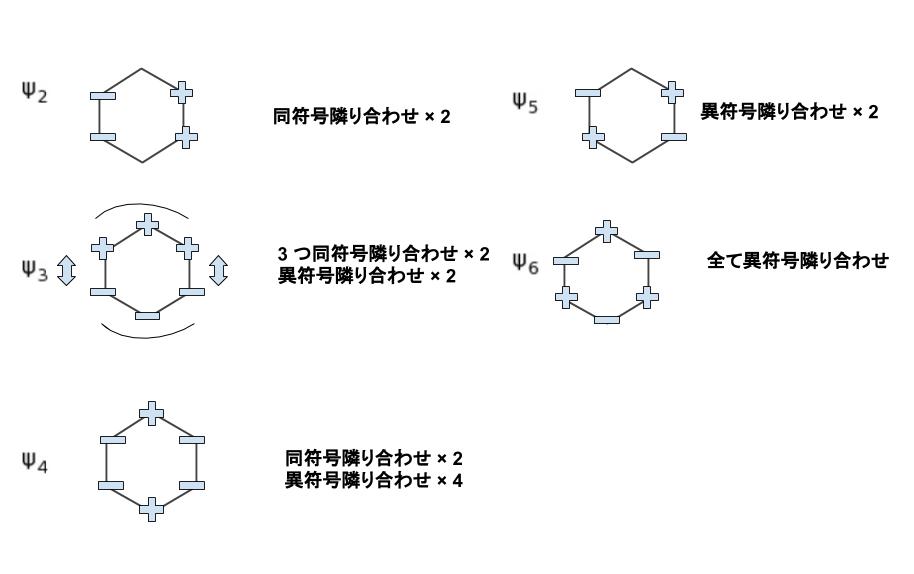
Ψ2 と同じエネルギー、つまり「同符号隣り合わせ × 2」ぐらい安定と思われるのは、Ψ3 です。
以上より、正解は 2 です。(ちなみに、Ψ4 と Ψ5 も同じエネルギーだろうと読み取れます。)

コメント