問 題
気体分子の運動に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当な
のはどれか。
「N 個の理想気体の分子が体積 V の中にあるとき、衝突頻度 z は
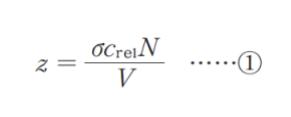
と表すことができる。ここで σ はこの気体分子の衝突断面積である。また、crel は気体分子の相
対平均速さであり、気体分子の平均の速さ c との間には、crel = ㋐ の関係がある。式 ① は圧力 p、温度 T、ボルツマン定数 kB を用いると、z = ㋑ と表すことができる。」

正解.3
解 説
気体分子の「相対的速さ」ということなので、2つの気体分子を、ベクトルで考えてみます。

余弦定理より
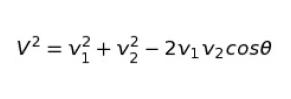
気体全体を考えれば、v1、v2 は全部平均の速さとおいてよいと考えられます。v1 = v2 = c です。また、θ も平均すれば、ランダムなので 0 でよいと考えられます。以上より、V2 = 2c2 です。∴ V = √2c です。㋐ は√2c なので、正解は 1 ~ 3 です。
㋑ですが、Na をアボガドロ定数として、kB = R/Na です。これは基礎知識です。理想気体の状態方程式 pV = nRT です。N 個の理想気体分子なので、物質量 n = N/Na と表すことができます。代入すると pV = (N/Na)RT です。 式を変形すれば N/V = pNa/RT なので、N/V = p/kBT と表すことができます。① に代入すれば、z = σcrelp/kBT です。
以上より、正解は 3 です。

コメント