微分方程式

y=f(x) について、x,y,y’ に関する方程式を微分方程式といいます。微分が含まれる方程式と考えればよいです。

例）y’ = 2x + 1 → y = x² + x + C
例）y’ = y → y = Ce^x

微分方程式を解く
つまり y = ~ の形に直す際、任意定数 C を含む形を一般解といいます。微分方程式はそもそも解ける形と解けない形があります。さらに、微分方程式だけからは一般解しか求まりません。

微分方程式に加え
ある(x,y) について満たすべき初期条件や境界条件が与えられることがあります。その際は C が一意に定まります。C を含まない形の解を特殊解と呼びます。

例）y’ = 2x + 1、(x,y) = (0,1) を満たす
→ y = x² + x + 1 が特殊解となります。

一般に
dy/dx = f(x)g(y) で表される形の微分方程式を変数分離型と呼びます。変数分離と呼ばれる操作を用いて解けます。変数分離とは、f(x)dx = g(y)dy のように、式の片方に一方の文字を集めて分離するような式変形のことです。

薬学において重要な微分方程式は
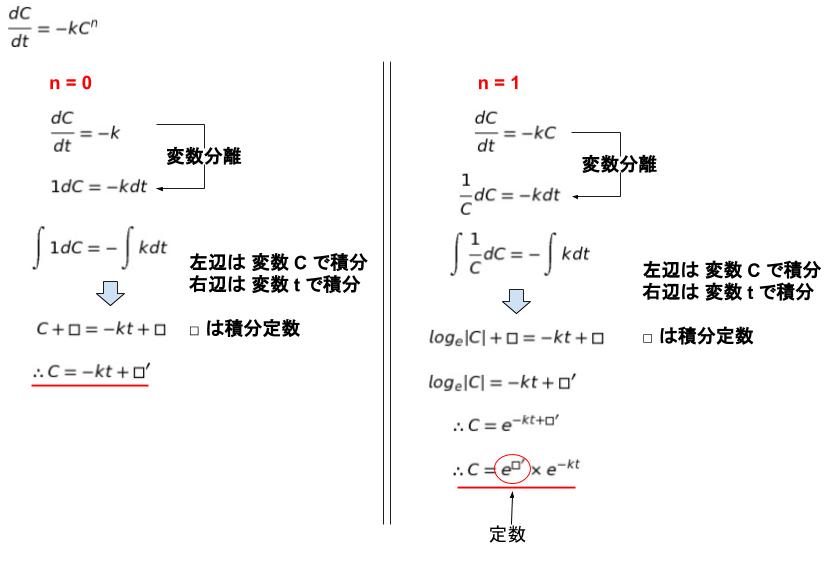
血中濃度に関する速度反応式です。dC/dt = -kCⁿ ・・・（１）で表されます。t は時間、C は薬物濃度です。k,n は定数です。特に k を反応速度定数、n を反応次数と呼びます。変数分離型の微分方程式なので、解けます。

（１）の n = 0,1,2 の場合について
結論は 『C = ~』となります。以下、それぞれの微分方程式の式変形です。変数が C なので、積分定数を □ で表し、定数同士の計算で値が変わった場合を □’ としています。dC/dt を分数のように扱える点を意識し、変形を再現できるようにするとよいです。