気体の分子運動とエネルギーの関係

気体分子は、たえず動き回っています。言い換えると、運動しています。そして、分子は全てが同じ速さで運動しているわけではありません。ある温度 T において、１つ１つの分子に注目してみると、ある分子はゆっくりと、ある分子は速く運動しているということです。これを分子の速さの分布といいます。

温度 T のある瞬間において、「特定の速さ v で動いている、質量 m の分子の割合」に関する式が、マクスウェルにより導かれています。マクスウェルの速度分布と呼びます。以下のような式です。 m,T によりグラフが変化するのですが、グラフの１例も示します。

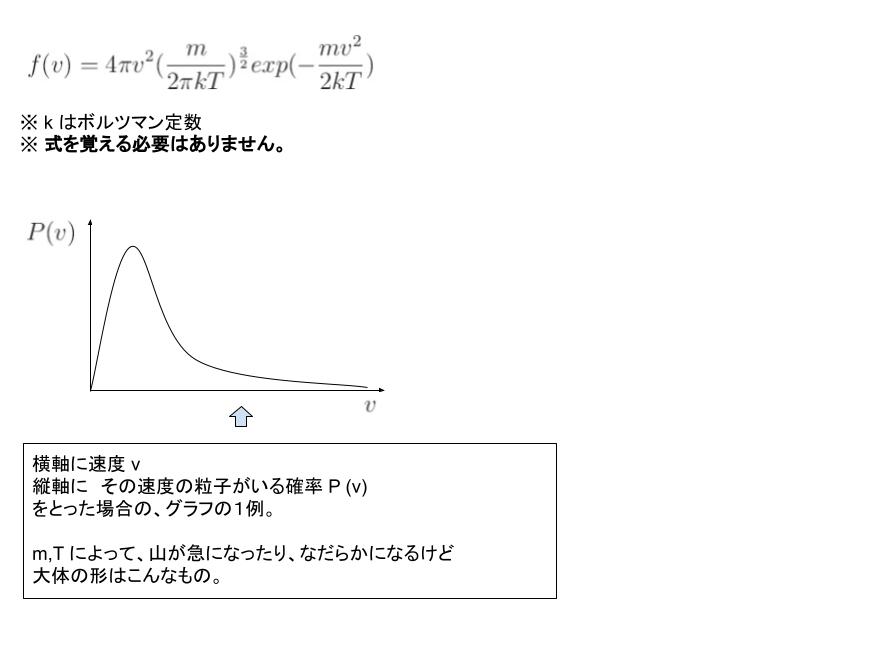分布確率における最大値をとる速さが「最確の速さ」と呼ばれます。上のグラフでいうと、P(v) が最大値をとっているような v のことです。その他に「平均の速さ」や「二乗平均の速さ」に注目する場合もあります。どの速さも、温度の平方根に比例するという特徴があります。

ちなみに
運動エネルギー E = mv²/2 であることから、気体分子の平均運動エネルギーを求めることができます。気体分子の平均エネルギーは 3kT/2 と表されます。

気体分子の運動エネルギーは大きく３つに分類できます。すなわち並進運動エネルギー、回転運動エネルギー、振動運動エネルギーです。