問 題
下の図は、マクスウェル・ボルツマン分布則に基づいた、温度の異なる、ある理想気体の運動の速さ分布である。図中の曲線Aは温度T1=150Kの場合、曲線Bは温度T2の場合を示す。気体の運動に関する記述のうち、正しいのはどれか。2つ選べ。ただし、図中の分子運動は並進運動のみを表しているものとする。
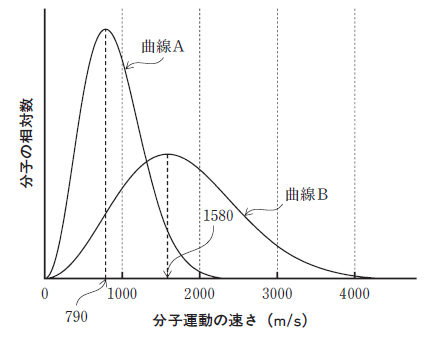
- T2は、約300Kである。
- 各曲線における最大確率速度(頂点における速度)は、それぞれの平均の速さより小さい。
- 分子量が2倍、温度T1の理想気体における分布曲線は、曲線Aと比べて、右側にシフトし広がる。
- 温度が高くなれば、速さ分布は広がる。
解 説
選択肢 1 ですが
最大確率速度(最確速度)は、温度 T の平方根に比例します。つまり、最確速度が 2 倍になる時温度は 4 倍です。T1 が 150 ℃なので、T2 は、600 ℃になります。300 ℃では、ありません。よって、選択肢 1 は誤りです。
選択肢 2 は、その通りの記述です。
選択肢 3 ですが
分子量が大きくなると、分布曲線は左にシフトし、シャープになります。イメージとしては、同じ温度であっても軽いものなら、激しく動くこともあるけれど重たいものだと、みんなほとんど動かないということです。
また別のたとえとして、温度が低い→素人の微妙なコントが放送されている。温度が高い→名人のとてもおもしろいコントが放送されている。分子量が小さい→お笑いをほとんど知らない集団が聞いている。分子量が大きい→お笑い通の集団が聞いている。ある分子の速度→コントを聞いて、うけた度合い とします。
するとこの時、温度が低い=微妙なコント でも、まだお笑いを知らない集団の中にはめちゃくちゃうける人も、案外いる。(速度が大きい分子も、案外いる。)しかしお笑い通の集団では、まぁうけない。(分布が左による。)微妙なコントでめちゃくちゃうける人なんてめったにいない。(分布に広がりはなくなる。シャープになる。)というイメージです。よって、選択肢 3 は誤りです。
選択肢 4 は、その通りの記述です。
以上より、正解は 2,4 です。

コメント