薬剤師国家試験第110回問175 過去問解説

　問題　　　　　

体内動態が線形 1 – コンパートメントモデルに従い、生物学的半減期が 1.4 時間である薬物を、3 種類の剤形で同用量を経口投与したとき、下表に示す血中濃度時間曲線下面積 (AUC) と一次モーメント時間曲線下面積 (AUMC) が得られた。

この結果に関する記述として、正しいのはどれか。2 つ選べ。

ただし、絶対的バイオアベイラビリティはいずれも 100 % とし、ln2 ＝ 0.693 とする。

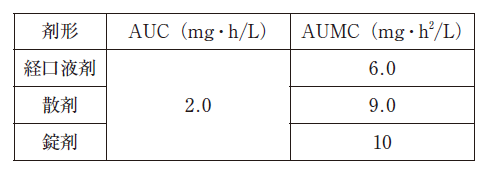
最高血中濃度が最も大きいのは経口液剤である。
投与量を増やすと平均滞留時間は長くなる。
経口液剤を経口投与したときの平均吸収時間は約 1.0 h である。
散剤の平均溶出時間は約 0.5 h である。
錠剤の平均崩壊時間は約 1.5 h である。

正解．1, 3

　解説　　　　　

選択肢 2,4,5 が誤りと判断したい問題です。

選択肢 1 は妥当です。
横軸に時間、縦軸に血中濃度をとったグラフを考えます。AUC が同じであれば、吸収が速くて濃度がぐっと上がる方が最高血中濃度が高くなるだろう → 経口液剤が最も大きいだろう　という流れで選べるとよいです。

選択肢 2 ですが
「経口時の MRT=1/ka + 1/ke」が公式です。MRT は、ka 及び ke という、薬物及び人に依存する定数に関係づけられています。一方、投与量には依存していません。従って「投与量を増やすと平均滞留時間は長くなる」わけではありません。選択肢 2 は誤りです。

選択肢 3 は妥当です。
公式：「平均吸収時間 MAT = 経口時 MRT －静脈投与時 MRT」です。経口液剤の MRT は 6.0/2.0 = 3.0 です。(選択肢 4,5 解説で詳細)。

そして、静脈投与時の MRT ですが、これは MRT = 1 / ke という関係が成り立ちます。これを知らないと求められません。知らなかった場合は他の選択肢から判断するとよいです。

ke は、T_1/2 = ln2/ke (公式)、ln2 ≒ 0.7 より
1.4 = 0.7/ke、∴ ke = 1/2
→ 静脈投与時の MRT = 1/(1/2) = 2
→ 経口液剤の MAT = 3.0 － 2 = 1 です。

選択肢 4,5 ですが
「平均滞留時間（MRT） = AUMC/AUC（公式）」です。

従って
液剤の場合 6.0/2.0 = 3 h、散剤の場合 9.0/2.0 = 4.5 h、錠剤の場合 10/2.0 = 5 h です。

錠剤 → 散剤となるまでの「平均崩壊時間」が 5 － 4.5 = 0.5 h となります。散剤 → 液剤となるまでの「平均溶出時間」が 4.5 － 3 = 1.5 h です。選択肢 4,5 は誤りです。

以上より、正解は 1,3 です。

類題 106-48
https://yaku-tik.com/yakugaku/106-048/

類題 101-172
https://yaku-tik.com/yakugaku/101-172/

参考　モデルによらない薬物動態の解析法
https://yaku-tik.com/yakugaku/yz-3-1-9/

コメント