問 題
生体膜の膜電位は、膜の両側におけるイオン濃度の不均衡によって生じる。そのイオン濃度の不均衡は、生体膜が水や小さいイオンは通すが、大きなイオンは通さない半透膜の性質をもつことで生じる。
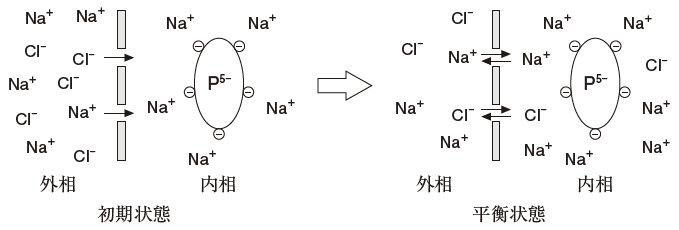
図のように、半透膜の内相にタンパク質 P5-(-5 の電荷をもち 5Na+ が対イオンとなっている) の0.01 mol/L 水溶液を置き、外相には濃度が 0.1 mol/L の NaCl 水溶液を置いておく。平衡状態に達したとき、半透膜の外相と内相の Na+と Cl- の濃度には次式が成立している。
[Na+]外相・[Cl-]外相=[Na+]内相・[Cl-]内相
平衡に達したときの半透膜の内相と外相の Na+の濃度の差に最も近い値はどれか。1 つ選べ。ただし、浸透圧差に基づく物質の移動は考慮しないものとする。
- 0.01 mol/L
- 0.03 mol/L
- 0.05 mol/L
- 0.07 mol/L
- 0.09 mol/L
解 説
初期状態において
外相 Na+・・・ 0.1 mol/L 、Clー・・・ 0.1 mol/L
内相 Na+・・・ 0.01 × 5 mol/L 、Clー・・・ 0 mol/L です。
平衡状態において
外相から内相に Na+、Clー が移動し、x mol/L 濃度が減少したとします。すると、外相の減少分だけ、内相において濃度が増加します。
従って、平衡状態において
外相 Na+ ・・・ 0.1 ー x mol/L、Clー・・・ 0.1 ー x mol/L
内相 Na+・・・ 0.05 + x mol/L、Clー・・・ x mol/L です。
問題文より
[Na+]外相・[Cl-]外相 = [Na+]内相・[Cl-]内相
であるから
(0.1 ー x)・(0.1 ー x) = (0.05 + x)・x が成立します。展開して、x を求めると x = 0.04 です。計算過程は、以下のようになります。
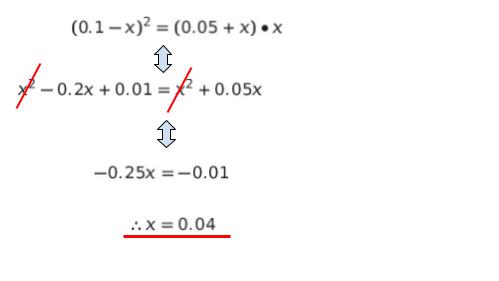
x = 0.04 を代入すれば、平衡状態において Na+ は 外相が 0.06 mol/L、内相が 0.09 mol/L です。従って、濃度差は 0.09 ー 0.06 = 0.03 とわかります。
以上より、正解は 2 です。

コメント