指数関数、対数関数

ルールが決まっていて、ある値を投げると、ルールに基づき処理された数が帰ってくるような関係を関数といいます。y = f(x) のように書いたりします。ルールの例は「投げてこられた値を 2 倍して返す（y = 2x) 」です。

指数関数は、y = a^x と書ける関数です。
a は定数です。a = 2 を例にあげると y = 2^x となります。指数関数の特徴は大きく３点です。『１：x = 0 の時 y = 1 を必ず通る』、『２：a > 0 かつ、a ≠ 1 とする』、『３：a の値によって、x が増えた時に y がどうなるか大きく 2 分される。具体的には 0 < a < 1 の時は、x 増えると y は小さくなる。a > 1 の時は、x 増えると y 増える』です。

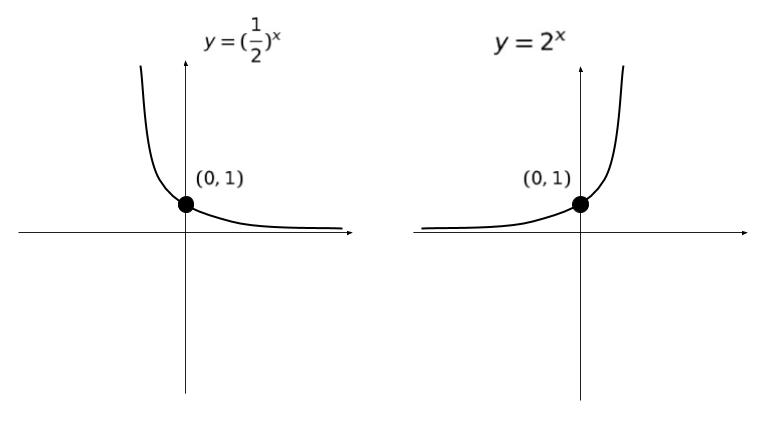
急速に増加 or 低下するので、細胞分裂や半減期などを表すことができる形式です。代表的な y = (1/2)^x と、y = 2^x のグラフを以下にあげます。

対数関数は、y = log_aX と書ける関数です。
a は定数です。a = 2 を例にあげると y = log₂X です。対数関数の特徴は大きく３点です。『１：x = 1 の時、y = 0 を必ず通る。』『２：a > 0 かつ a ≠ 1、X > 0 である。』『３：a の値によって、x が増えた時に y がどうなるか大きく 2 分される。具体的には 0 < a < 1 の時、0 < a < 1 の時は、x 増えると y は小さくなる。a > 1 の時は、x 増えると y 増える』です。

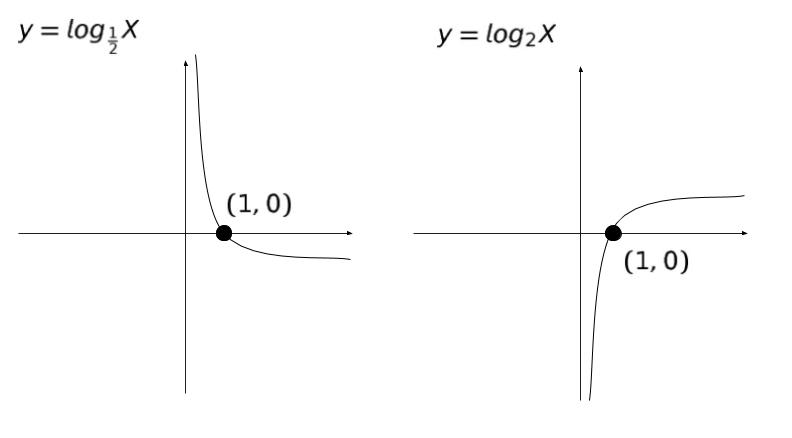
非常にゆっくり増えたり減ったりするので、特に一方の変数が非常に大きな値や小さな値をとる時に用いると便利な形式です。pH や吸光度について表す時に用いられます。代表的な y = log _1/2 Xと、y = log ₂ X のグラフを以下にあげます。

指数・対数でよく使う公式と例　一覧