問 題
ある薬物を患者に点滴静注により持続投与中である。定常状態における血中薬物濃度は 5.0 μg/mLであり、定常状態到達時にいったん完全に排尿し、5 時間後に再度排尿した尿の総量は 300 mL、尿中薬物濃度は 180 μg/mL であった。
この患者における糸球体ろ過速度を 120 mL/min、薬物の尿細管再吸収率を 20%、血中非結合形分率を0.20 としたとき、この薬物の尿細管分泌クリアランス (mL/min) に最も近い値はどれか。1 つ選べ。
- 10
- 20
- 150
- 600
- 2,500
解 説
定常状態における血中濃度が与えられているので、まずは Css = (D/τ)/CL を思い出します。本問では使いませんが、この連想は必須です。
定常状態到達時、いったん完全排尿し、5時間後再度排尿し、300mL、尿中濃度 180 μg/mL とあります。5h で、300 × 180 = 54000 μg の薬物が尿中排泄されたとわかります。
次に、糸球体ろ過速度が 120mL/min に注目します。5h = 300 min で 36000mL 血液が糸球体ろ過されるということです。
血中非結合分率 0.20 です。血中薬物濃度が 5.0 ですが、非結合しか糸球体ろ過通過しないので、原尿の薬物濃度は 1.0 μg/mL とわかります。つまり、糸球体ろ過分のみに注目すれば 5h で薬物が 36000 × 1.0 = 36000 μg 排出されるとわかります。これに分泌を受け、その後再吸収された結果が 54000 μg であればOKということです。以下のようなイメージです。
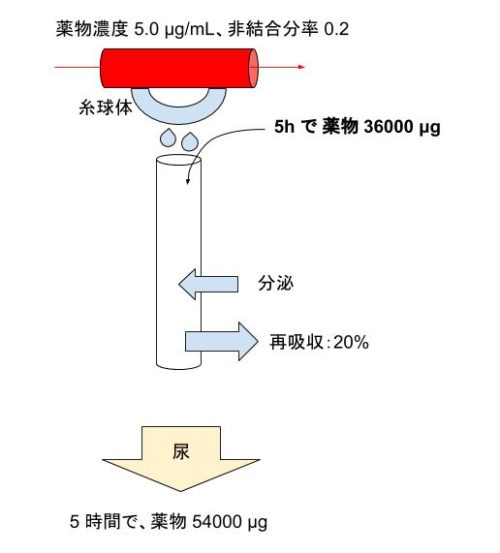
ということは再吸収を受ける前が 54000 ÷ 0.8 = 67500 であればよいとわかります。
従って、分泌される薬物の量が 67500 ー 36000 = 31500 μg とわかります。1 分当たりであれば 300 で割って 105 μg です。分泌される薬物濃度は血中薬物濃度と同じと考えられるため 105 ÷ 5 = 21mL/min が分泌クリアランスです。最も近いのは 20 です。
以上より、正解は 2 です。
類題 101-44
参考 薬剤学まとめ 腎クリアランス

コメント