問 題
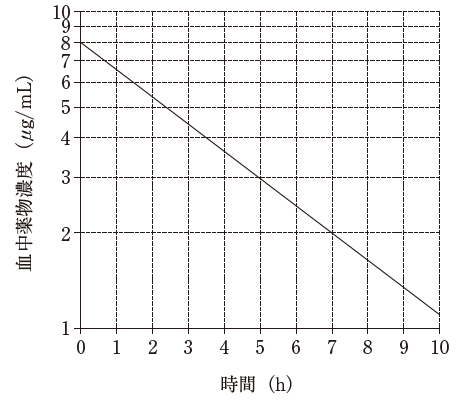
肝代謝のみで消失する薬物 400 mgをヒトに単回静脈内投与した際、図に示す血中濃度推移が得られた。この薬物の体内動態は線形性を示し、経口投与時に門脈血中に移行する割合は100%である。この薬物を反復経口投与し、定常状態での平均血中薬物濃度を3.5 μg/mLとしたい。
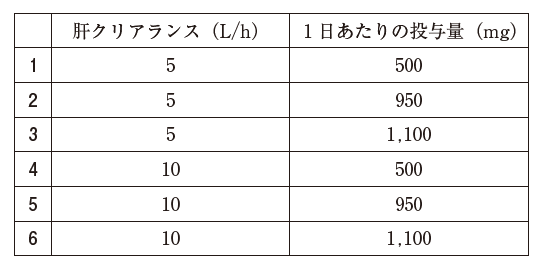
この薬物の肝クリアランス (L/h) 及び1日あたりの投与量 (mg) の組合せとして最も適切なのはどれか。1つ選べ。なお、肝血流速度は80 L/h、ln2 = 0.693 とする。
解 説
以下の公式は基礎知識です。
Vd = D/C0 ※静注時。
T1/2 = ln2/ke ※ ln2 ≒ 0.7 として OK
CL = ke・Vd
図の血中濃度推移における、時間 0 に注目すると、血中薬物濃度 8 です。従って、Vd = 400 mg/8 μg/mL となります。400mg = 400000μg です。Vd = 400000/8 = 50000 mL となります。単位を L になおすと、Vd = 50L です。
次に、図の血中濃度推移から、半減期(T1/2) が 3.5h と読み取れます。すると、ke = 0.7/T1/2 なので、ke = 0.2 です。CL = 0.2 × 50 = 10 とわかります。正解は 4 ~ 6 です。
定常状態の血中薬物濃度と来れば、Css = (D/τ)/CL を思い出します。τ は投与間隔です。聞かれているのが 1 日あたりの投与量なので、τ = 24(h) を代入して計算します。3.5 = (D/24)/10 です。左辺の単位である μg/mL = mg/L なので、右辺の数値に関して単位変換不要です。3.5 = D/240 なので、D = 840 とわかります。
ここで、反復「経口」投与なので、投与量が全て体循環に入るわけではない点が、最後のポイントになります。肝血流速度が 80L/h で、肝クリアランスが 10L/h だから、抽出率 E が 1/8 です。従って、経口投与した薬物のうち、1/8 は初回通過効果で代謝され、残りの 7/8 が体循環に入ります。体循環に入る量が 840 なので、840 × 8/7 = 960 が1日あたりの投与量です。一番近いものを選ぶと 950 となります。
以上より、正解は 5 です。

コメント