問 題
一般に、薬物粉末の粒子径が小さいほど薬物の溶解速度が大きくなる理由として最も適切なのはどれか。1つ選べ。
- 飽和溶解度の増大
- 比表面積の増大
- 粒子表面の拡散層の減少
- 薬物分子の拡散係数の増大
- 飽和層と内部溶液の薬物濃度差の減少
正解.2
解 説
本問の解き方を、2つ紹介します。1つめは、薬剤学で、溶解速度 と来たので、ネルンスト-ノイエス-ホイットニーの式(下図参照)を使う方法です。

左辺が溶解速度です。右辺において、D は拡散係数、S は固体の(比)表面積、V は溶液の体積、δ は拡散層の厚さです。V や δ は溶液側の話なので今回は無視します。
拡散係数 D は更に
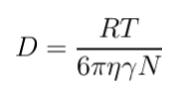
で表されます。R、πは定数です。ηは溶液の粘度なので、無視します。Tは温度です。問題に記述がないので、無視します。以上より、本問において D に影響を与えるのは、r 及び N です。r は粒子の半径です。N はアボガドロ数です。
粒子径が小さくなると、r が小さくなり、分母が小さくなるから全体は大きくなります。ですが、r が小さくなれば粒子の数 N がその分増えているはずなので D はそれほど変化がないか、むしろ大きくなっていると考えられます。
一方で、同じ重さの固体を考えると粒子径を小さくして、小さなつぶをいっぱいにすれば(比)表面積 S は大きくなります。従って、溶解速度が大きくなる理由としては、Sの増加、つまり比表面積の増加 が適切です。
以上より、正解は 2 です。
2つめの解き方としては、式で深く考えず
例えばコーヒー豆を挽いて粗くすると、水 → コーヒーがあっという間なのはなぜか? 豆を挽いて表面積が多くなって水といっぱい接触するから、という感じで荒っぽく考えて、表面積の増加だから正解は 2 と考えるという方法です。
どちらの考え方もできるようにしておくと、様々な問題に対応できるのではないかと思います。

コメント