問 題
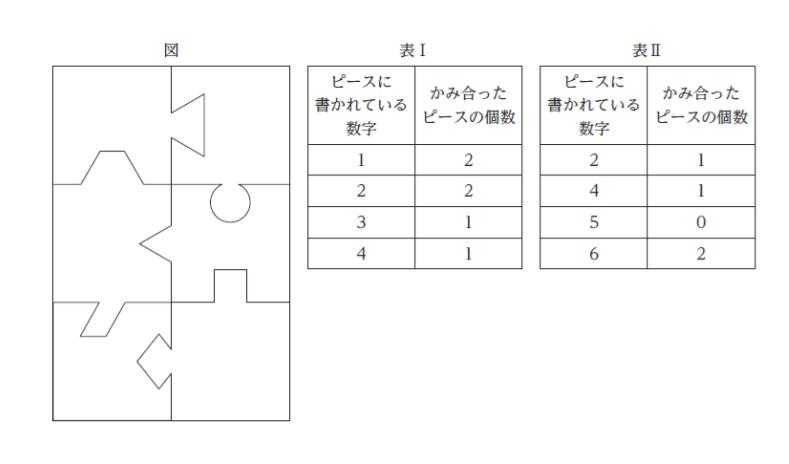
ジグソーパズルの六つのピースがあり、それぞれの表面に1 ~ 6 の数字が一つずつ書かれている。これらのピースを正しくかみ合わせると、図のような縦 3 ピース、横 2 ピースの長方形になることが分かっている。
そこで、どのピースとどのピースがかみ合うかどうかを確かめるために、 1 ~ 4 の数字が書かれた4 種類のピースのみを用いて全ての組合せを試した結果は、表Ⅰのようになり、また、 2 、4 、 5 、 6 の数字が書かれたピースのみを用いて全ての組合せを試した結果は、表Ⅱのようになった。
このとき、 1 の数字が書かれたピースとかみ合うピースに書かれている数字を全て足し合わせると、その値はいくらか。
1. 8
2. 9
3. 10
4. 11
5. 12
解 説
表Ⅰに注目します。
「数字1が書かれたピース」が「数字2が書かれたピース」がかみ合わなかったとします。すると、かみ合ったピースの個数が 2 個だから、1-3、1-4が噛み合ったことになります。
同様に、数字2が書かれたピースも、2-3、2-4が噛み合ったことになります。すると、数字3、4が書かれたピースは最低2個噛み合ったことになってしまいます。これは表Ⅰと矛盾します。従って、1-2は噛み合ったとわかります。
次に、表Ⅰ、Ⅱに共通して現れている数字2、4の組に注目します。
もしも 2-4が噛み合うとすると、表Ⅱにおいて 6 と噛み合うものがなくなってしまいます。これは表Ⅱと矛盾します。従って、2-4は噛み合わなかったとわかります。その結果、2-6、4-6が噛み合ったとわかります。
表Ⅰに戻ってみれば、1-2、1-4が噛み合ったとわかります。また、2-3が噛み合ったとわかります。
表Ⅰ、Ⅱに共通している数字2、4に改めて注目すれば、2は3つ噛み合うピースがあり(2-1、2-3、2-6)、4は2つ噛み合うピースがある(4-1、4-6)とわかります。
3つ噛み合うピースは図における真ん中の行の2つのどちらかです。そこと噛み合っていないピースのうち一つが4なので、一例として、以下のような 2,4 の配置が考えられます。
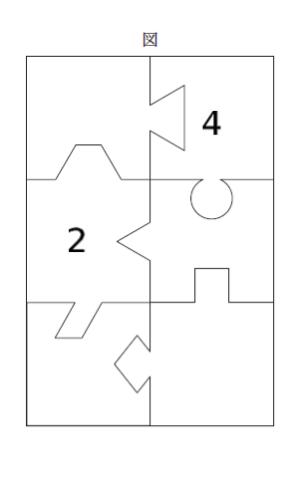
選択肢も活用すれば、2の上及び2の下に 1 を配置できないことがわかります。なぜなら、1と噛み合うピースの数字の和が 最低の8にも至らないからです。※ 2 の下に1、1の右に6の可能性については「2-6」の組が確定しているのでありえません。
従って、2の右が1です。2の上が6、2の下が3です。残りが5となります。従って、1の数字が書かれたピースとかみ合うピースの数字を全て足すと、2+3+5 = 11です。
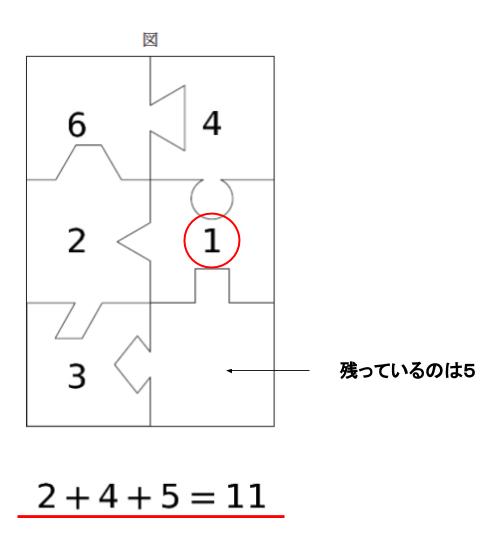
以上より、正解は 4 です。

コメント