問 題
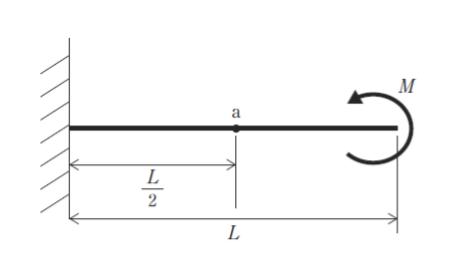
図のように,長さ L の片持梁の自由端に曲げモーメント M が作用するとき,点 a でのたわみ角と変位(たわみ)の組合せとして最も妥当なのはどれか。
ただし,梁の断面は一様であり,断面二次モーメントは I ,ヤング係数は E とする。
また,梁の自重及びせん断変形は無視できるものとし,たわみは微小であるものとする。なお,梁のたわみ曲線の微分方程式は,水平右向きの座標を x,鉛直下向きのたわみを y,位置 x での曲げモーメントを Mx とすると,次式で表される。

正解 (3)
解 説
点 a で仮想切断して考えれば、M の曲げモーメントが a 点でもかかっているということがわかります。
たわみ角とは、接線の傾きです。つまり dy/dx です。問題文に与えられている式の両辺を1回 x で積分すれば dy/dx = -Mxx/EI です。Mx = M、x = L/2 を代入すれば -ML/2EI です。
次にたわみは y です。dy/dx = -Mxx/EI をもう一度両辺 x で積分すれば y = -Mxx2/2EI です。Mx = M、x = L/2 代入すれば -ML2/8EI です。
以上より、正解は 3 です。

コメント