問 題
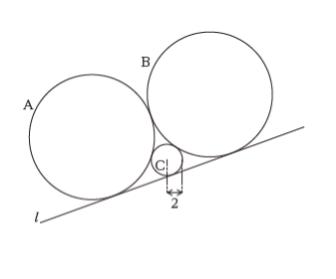
図のように,円A,B,Cと直線 l が互いに接している。円Aと円Bの半径が等しく,また,円Cの半径が 2 であるとき,円Aの半径はいくらか。
1. 4√3
2. 7
3. 8
4. 6√2
5. 9
正解 (3)
解 説
斜めだとわかりにくいので、まっすぐに直します。
円がでてきたら、中心同士や、中心と特徴的な点を結びまくると方針が見えてくることが多いです。そこでまず、大きい円と小さい円の中心等を結んでみています。
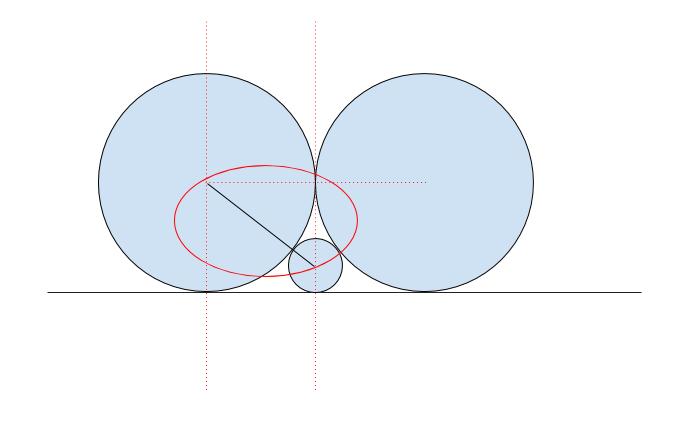
すると、大きい円の半径を r とおけば、「r ー 2」、「r」、「r + 2」 を3辺の長さとする直角三角形が見つかります。(赤丸部分)。以下、解法を 2 通りあげます。両方で考えることができるようにしておくとよいと思います。
1【三平方の定理】
(r + 2)2 = (r ー 2)2 + r2
→r2 ー 8r = 0 ∴ r = 8。
2【選択肢の活用】
選択肢を見れば、 r = 8 の時、3辺の長さが「6,8,10」となって、代表的直角三角形の辺の比の一つである「3:4:5」となり、これが正解と考えられます。
以上より、正解は 3 です。

コメント