問 題
ある経済の生産関数が
Y=2√N (Y:総生産量,N:雇用量)
で与えられているものとする。いま,名目賃金率 W が 4 で一定であり,雇用量が労働需要曲線上で決定されているものとする。
このとき,この経済の総供給関数として妥当なのはどれか。ただし,古典派の第一公準は満たされており,P は物価水準を表すものとする。
1.Y = 8P
2.Y = 2P
3.Y = P
4.Y = P/2
5.Y = P/8
正解 (4)
解 説
経済における労働市場は、企業の利潤最大化行動から導出できます。このような考え方の下、利潤最大化条件を求めると、労働の限界生産力と、実質賃金(名目賃金÷物価)が等しい時に利潤最大化となることが知られています。従って、この点において労働雇用量が決定される、という内容が「古典派の第一公準」です。
生産関数が Y = 2√N なので、限界生産を、生産関数を微分して求めると、以下のようになります。

古典派の第一公準より、限界生産力と実質賃金 (W/P) が等しいため、1/√N = 4/P ・・・(1)が成り立ちます。そして、1/√N は、Y を用いて表すことができるため、(1)を書き換えれば、Y と P の関係式を得ることができます。計算は、以下のようになります。
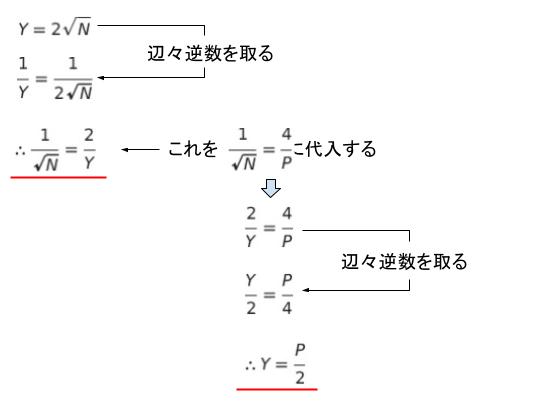
以上より、正解は 4 です。

コメント