H29年 国家一般職(高卒 技術) No.63 土木基礎力学　解説

　問 題　　　　　

直径 20 mm の一様な円形断面の鋼材に 50 kN の引張力を加えたところ，鋼材の直径は 5.0 × 10^-3 mm 細くなった。この鋼材のポアソン比はおよそいくらか。ただし，鋼材のヤング係数を 2.0 × 10⁵ N/mm²，円周率を 3.14 とする。

1． 0.1
2． 0.2
3． 0.3
4． 0.4
5． 0.5

 

 

 

 

 

　解 説　　　　　

ひずみについては
・軸方向力を P、断面積 A とすると、軸応力 σ は P/A です。
・力を加えて、元々 長さ l の物体が Δl 伸びた時、ひずみ ε を Δl/l で表します。
この時、E をヤング係数（ヤング率）として
σ = Eε が成立します。ここまでが基礎知識です。

ポアソン比とは
部材を引っ張って伸ばした時の引張方向のひずみと、垂直方向のひずみの比です。例えばポアソン比が 0.1 であれば、「縦に１mm のびたら、横に 0.1mm 縮む」ということです。

直径 20 mm の円形断面なので、まず断面積 A = π × 10² です。50kN の引張力を加えているため、応力 σ  = 50000/100π です。

σ = Eε なので 50000/100 π = 2.0 × 10⁵ × ε です。
∴ ε = 1/400 πです。

この時、横方向のひずみは
直径が 20mm で、5.0 × 10^-3 mm 細くなっているので
5.0 × 10^-3/20 です。

ポアソン比は、横方向のひずみ／縦方向のひずみ　なので
(5.0 × 10^-3/20)  /（1/400 π） で求めることができます。分母・分子に 400 πかければ約 0.3 です。

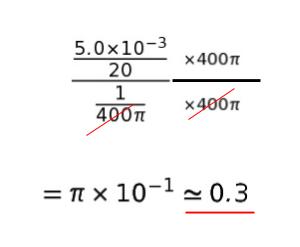
以上より、正解は 3 です。